यहाँ हमने Class 11 Physics Chapter 13 Notes in Hindi दिये है। Class 11 Physics Chapter 13 Notes in Hindi आपको अध्याय को बेहतर ढंग से समझने में मदद करेंगे और आपकी परीक्षा की तैयारी में सहायक होंगे।
Class 11 Physics Chapter 13 Notes in Hindi अणुगति सिद्धांत
परमाणु :- पदार्थ / द्रव्य की मूल इकाई परमाणु होती है जिसके मूल
- इलेक्ट्रॉन
- प्रोटॉन
- न्यूट्रॉन
अणु (यौगिक या तत्व):- परमाणु का समूह अणु कहलाता है।
पदार्थ
- अणुओं का समूह पदार्थ कहलाता है।
- पदार्थ में परमाणुओं व अणुओं के मध्य कार्य करने वाले बल क्रमशः – अन्त: परमाण्विक व अन्त: आण्विक होते है।
- जिनकी प्रकृति विद्युत चुम्बकीय होती है।
पदार्थ की अवस्था :-
- (i) ठोस (solid)
- (ii) द्रव (liquid)
- (iii) गैस (Gas)
मुख्य गुण:-
- ठोस – प्रत्यास्थता
- द्रव – श्यानता , पृष्ठ तनाव, संपीड़यता
- गैस – श्यानता, पृष्ठ तनाव, तरल (न्यून)
दृढ पिण्ड :- वह ठोस पिंड जिस पर बाह्य बल लगाने से उसकी आकृति व आकार दोनों अपरिवर्तित रहे अर्थात् अन्त: परमाण्विक व अन्त: आण्विक दूरियाँ अपरिवर्तित रहे।
Note :- व्यवहार में ऐसा पिण्ड मिलना असंभव है।
Quarts (पूर्ण प्रत्यास्थ है)
गैस
जिन पदार्थों में कण दूर-दूर व स्वतंत्र हो उसे गैसीय अवस्था कहते हैं।
गैस के अध्ययन हेतु आवश्यक स्थूल कारक (चर) –
- दाब (P)
- ताप (T)
- आयतन (V)
गैस या मापन हेतु आवश्यक कारक :-
- मोल
- आवोगाद्रो की संख्या
- अणु भार या परमाणु भार
- मोलकता व मोलरता
गैस के स्वरूप :-
- वास्तविक गैस
- आदर्श गैस
P,V व T में सम्बन्ध:-
- आदर्श गैस अवस्था समीकरण → PV= nRT
- वांडरवाल समीकरण → \(p+ \frac{q}{v^2}\)(v-h)= nRT
PV = nRT की सार्थकता:-
यह आदर्श गैस के लिए P,V व T में सम्बन्ध है जो आदर्श गैस अवस्था समीकरण कहलाता है।
Note :- आदर्श गैस :- वे सभी गैसें जो PV= nRT का पालन करे, वे आदर्श गैस कहलाती है।
विशेष:- कम घनत्व वाली सभी वास्तविक गैस उच्च ताप व निम्न दाब पर आदर्श गैसों की तरह व्यवहार करती है।
n Means :- मोलों की संख्या ।
Chapter 2: मात्रक और मापन
Chapter 3: सरल रेखा मे गति
Chapter 4: गति के नियम
Chapter 6: कार्य, शक्ति एवं ऊर्जा
Chapter 7: कणों के निकाय तथा घूर्णी गति
Chapter 10: तरल पदार्थों के यांत्रिक गुण
Chapter 11: द्रव्य के तापीय गुण
Chapter 14: दोलन गति
मोल
- पदार्थ (ठोस/ द्रव्य/गैस) की मात्रा 1 मोल कहलाती है।
- जिसमें परमाणु/अणु की संख्या आवोगाद्रो की संख्या के तुल्य हो।
मोलों की गणना:- अगर पदार्थ की मात्रा gm है तो
- मोलों की संख्या:- \(\frac{M}{N}\)
- अगर पदार्थ में परमाणु / अणु की संख्या (N) दी हो तो n = \(\frac{N}{NA}\)\
आवोगाद्रो संख्या (NA):- 1 मोल (1 gm. mol) पदार्थ में परमाणुओं /अणुओं की संख्या आवोगाद्रो संख्या कहलाती है।
जिसका मान NA = 6.023 x 1023 प्रतिग्राम मोल
= 6.023 x 1026 प्रति kg mole
दी मात्रा (m) के किसी पदार्थ में परमाणु/ अणुओं की संख्या = \(\frac{m}{M}N_A\)
STP की सार्थकता
मानक ताप व दाब (Standard temperture and presure)
- मानक ताप = 0°c या 273.15K
- मानक दाब = 1 atm
STP पर 1 gm-mol गैस के लिए
- आयतन 22.4 लीटर होता है।
- परमाणु/ अणुओं की संख्या 6.023X1023 होती है |
गैसे के अणुगति सिद्धांत :-
- गैसीय अणु आकार व द्रव्यमान की दृष्टि से सर्वसम होते है।
- गैसीय अणु अनवरत यादृच्छ गति करते है।
- गैसीय अणुओं की चाल 0 से ∞ तक कुछ भी हो सकती है।
- गैसीय अणुओं का आयतन गैस के आयतन की तुलना में नगण्य होता है।
- इनके अणुओं के मध्य पूर्णत: प्रत्यास्थ टक्करें होती है।
- टक्कर से पूर्व अणु द्वारा सरल रेखा में तय दूरी मुक्त पथ कहलाती है।
- मुक्त पथों का औसत मान औसत मुक्त पथ / माध्य मुक्त पथ कहलाता है।
- अणुओं के मध्य किसी प्रकार का बल कार्य नहीं करता है। ( न आकर्षण न ही प्रतिकर्षण) । इस कारण अणुओं में स्थितिज ऊर्जा नहीं होती है।
- अणुओं में कुल ऊर्जा गतिज ऊर्जा के रूप में होती है।
- गैसीय अणुओं पर गुरुत्वाकर्षण बल का प्रभाव नगण्य होता है।
- कारण:- गैसीय अणुओं द्रव्यमान नगण्य होने के कारण गुरुत्वाकर्षण बल का प्रभाव नगण्य होता है। क्योंकि गुरुत्वाकर्षण बल द्रव्यमान के कारण लगता है।
गैस उस बर्तन की दीवारों पर दाब डालती है जिसमें यह भारी होती है।
कारण – क्योंकि गैसीय अणुओं के संवेग में परिवर्तन होता है।
बॉयल नियम
नियत ताप पर निश्चित मात्रा की गैस का दाब आयतन के या आयतन, दाब के व्युत्क्रमानुपाती होता है।
चार्ल्स नियम
“स्थिर दाब पर नियत मात्रा की गैस का आयतन ताप के समानुपाती होता है।”
गैलूसैक नियम
“स्थिर आयतन पर नियत मात्रा की गैस का दाब ताप के समानुपाती होता है।”
आवोगाद्रो का नियम
“नियत दाब (P) व ताप (T) पर एक समान आयतन वाली सभी गैसों में अणुओं की संख्या एक-समान रहती है।”
गैसों के विसरण संबंधी नियम
“इस प्रकार नियत दाब वाली गैस में विसरण की दर घनत्व के वर्ग मूल के व्युत्क्रमानुपाती होती है।”
यही विसरण का नियम है।
डॉल्टन का आंशिक दाब नियम
किसी ताप (T) पर बर्तन में भरी हुई भिन्न-भिन्न गैसों के मिश्रण का कुल दाब गैसों के भिन्न-भिन्न दाबो के योग के बराबर होता है।

जो पूरी गैस का दाब है। (मिश्रित गैस)
Note:- यही डॉल्टन का आंशिक दाब नियम है।
- “वह ताप जहाँ गैस के प्रतिअणु की औसत ऊर्जा शून्य हो जाए , परमशून्य ताप कहलाता है।”
- परम शून्य ताप से कम ताप होने पर किसी भी गैस को केवल दाब बढाकर द्रवित नहीं किया जा सकता।
वास्तविक गैसों के लिए वाण्डर वाल्स समीकरण :-
- वास्तविक गैसें सम्बन्ध PV = nRT का पालन तभी करती है जब उच्च ताप, निम्न दाब व गैसों का घनत्व कम हो।
- नियत ताप पर दाब (P) व आयतन (V) का गुणनफल नियत रहता है।
- परन्तु उच्च दाब व निम्न ताप पर वास्तविक गैसें उपरोक्त सम्बन्ध का पालन नहीं करती है।
इस हेतु वाण्डरवाल ने दो कारण बताए :-
- अणुओं का आयतन नगण्य नहीं माना जा सकता ।
- अणुओं के मध्य प्रतिकर्षण या आकर्षण बल को भी नगण्य नहीं मान सकते।
- अगर अणुओं के आयतन को b इकाई मान लें तो गैस द्वारा घेरा गया वास्तविक आयतन (V-b) होगा।
- अगर अणुओं में अंतराण्विक दूरियाँ एक नियत सीमा से कम हो तो प्रत्येक अणु अन्य अणुओं द्वारा आकर्षित होगा।
- वह अणु जो चारों ओर से अन्य अणुओं द्वारा घिरा हुआ है , उस पर नेट आकर्षण बल शून्य हो जाएगा लेकिन वह अणु जो दीवार के समीप है उस पर नेट आकर्षण बल शून्य नहीं होगा। यह बल बर्तन के अन्दर की ओर होगा।
- ऐसी स्थिति में कण के टकराने की गति कम हो जाएगी फलस्वरूप दीवार पर कम दाब उत्पन्न करेगा।
- यह दाब में कमी गैस के घनत्व के वर्ग के समानुपाती होगी परन्तु आयतन के वर्ग के व्युत्क्रमानुपाती होगा।
\(p= \frac{a}{v^2}\)(v-b) = nRT
जो वाण्डरवाल का समीकरण कहलाता है। जो वास्तविक गैसों पर लागू होता है। यहाँ a व b वाण्डरवाल नियतांक कहलाते है।
क्रान्तिक ताप (Tc)
”वह ताप जिससे कम ताप पर किसी भी गैस को केवल दाब बढ़ाकर द्रवित नहीं किया जा सकता है, क्रांतिक ताप कहलाता है।”
क्रान्तिक दाब (Pc)
”क्रान्तिक ताप पर किसी गैस को द्रव में बदलने हेतु आवश्यक दाब, क्रांतिक दाब कहलाता है।”
क्रान्तिक आयतन (Vc)
”क्रांतिक ताप व क्रांतिक दाब पर एक ग्राम मोल (gm.mol) गैस का आयतन, क्रांतिक आयतन कहलाता है।”
स्वातंत्र्य कोटी (Degree of Freedom)
गैस का प्रत्येक अणु मुक्त रूप से जितनी संभव दिशाओं में गति कर सकता है, उन दिशाओं की संख्या गैस के लिए स्वातंत्र्य कोटी कहलाती है।
चुकि गति की दिशा गति के प्रकार पर निर्भर करती है जो निम्न है :-
- स्थानान्तरीय गति (अधिकतम = 3 प्रकार की )
- घूर्णन गति (अधिकतम = 2 प्रकार की )
- कंपन गति (अधिकतम = केवल 1 उच्चताप)
Note :- ये गतियाँ अणुओं में परमाणुओं की संख्या पर निर्भर करती है।
| अणु | स्वातंत्र्य कोटी (f) |
|---|---|
| एक परमाण्विय [ He, Ne ] | f = 3+0+0 = 3 |
| द्विपरमाण्विय [ O2, N2, H2 ] | f = 3+2+0 = 5 |
ऊर्जा का समविभाजन नियम
ऊर्जा समविभाजन नियमानुसार गतिशील गैसीय अणु के लिए सभी स्वातंत्र्य कोटियों की ऊर्जा परस्पर एक समान होती है। इसका मान (½KBT) होता है।
ऊष्मा (Heat )
ऊष्मा का उपयोग:-
- आन्तरिक ऊर्जा में परिवर्तन
- बाह्य दाब के विरुद्ध कार्य करना पड़ता है।
विशिष्ट ऊष्मा
एकांक द्रव्यमान वाले द्रव्य के ताप में एकांक वृद्धि /कमी / परिवर्तन हेतु आवश्यक ऊष्मा, विशिष्ट ऊष्मा कहलाती है।
\(\frac{dQ}{dT}\)
स्थिर आयतन पर गैस की विशीष्ट ऊष्मा (Cv) = \((\frac{dQ}{dT})_v\)
स्थिर दाब पर गैस की विशिष्ट ऊष्मा (Cp) = \((\frac{dQ}{dT})_p\)
अर्थात् Cp > Cv
अत: स्थिर दाब पर विशिष्ट ऊष्मा, स्थिर आयतन पर विशिष्ट ऊष्मा से अधिक होते है।
Cp – Cv = R (मेयर सम्बन्ध)
\(\frac{C_p}{C_v}\) = y (गामा) (रुद्धोष्म निष्पति)
| गैस का स्वरूप | f | Cv | Cp =Cv + R | y=Cp/v |
|---|---|---|---|---|
| एक परमाण्विय | 3 | 3/2R | 5/2R | 5/3=1.67 |
| द्वि परमाण्विय | 5 | 5/2R | 7/2R | 7/5=1.4 |
| बहु परमाण्विय | (6+fv) | ½(6+fv)R | ½R(8+fv) | (8+fv)/(6+fv) |
गैस के लिए
- मुक्त पथ
- माध्य मुक्त पथ
- माध्य मुक्त पथ की निर्भरता

गैसीय अणु
(i) मुक्त पथ:- किन्हीं दो क्रमागत टक्करों के मध्य अणु द्वारा तय की गयी सीधी दूरी मुक्त पथ कहलाती है। सभी टक्करों के लिए इनका मान भिन्न-भिन्न होता है।
जैसे:- चित्र में λ1, λ2, λ3 ,—— है।
(ii) औसत मुक्त पथ:- गति के दौरान एक निश्चित समय अन्तराल में तय सभी मुक्त पथों का औसत मान, औसत मुक्त पथ कहलाता है।
(iii) माध्य मुक्त पथ की निर्भरता :-
माध्य मुक्त पथ के लिए सूत्र –
λ =\(\frac{1}{πd^2n}\)
λ की गणना (औसत मुक्त पथ)
- माना N अणु वाली गैस है, जिसका आयतन V है, तब आण्विक घनत्व “n ” = /(/frac{N}{v}/)
- गतिशील अणु गति के दौरान अपने व्यास के तुल्य त्रिज्या वाले बेलनाकार स्थान में आने वाले अणुओं से टकराएगा ।
- माना अणु का व्यास d है तब Δt समय में बनने वाले बेलनाकार स्थल का आयतन होगा:- πd2vΔt
- उपरोक्त स्थल के अणु होंगे :-

गैस का प्रसार गुणांक (α)
- ऊष्मा→ गैस→ प्रसारित (V में बढोतरी ] जब P स्वतंत्र हो (नियत)
- V नियत रखना → P को बढाओ
- आयतन व दाब में आनुपातिक परिवर्तन (ΔV/V या ΔP/P ) तापान्तर के समानुपाती होता है।
गैसों का अणुगतिक सिद्धान्त
गैसों के अणुगतिक सिद्धान्त की अवधारणाएँ या परिकल्पनाएँ :-
- गैसों के कण सभी संभव दिशाओं में सभी संभव वेगों के साथ लगातार गति करते है। जिसे ब्राउयनी गति (Zig-Zag motion) कहते है।
- इन कणों के मध्य आकर्षण बल नगण्य होता है।
- गैंसों का प्रत्येक कण ठोस व गोलाकार आकृति का होता है।
- दो अणुओं के मध्य टक्कर के समय तय की गयी रेखीय दूरी मुक्त पथ कहलाती है।
- मुक्त पथ या टक्कर के समय, लगा समय विश्रान्ति काल कहलाता है।
- इन कणों पर गुरुत्वाकर्षण बल का प्रभाव नगण्य होता है।
दाब का व्यंजक:-

वेगों का वर्ग माध्य मूल मान (Crms)
जब किसी गैस के अणुओं के वेगों के वर्गों का माध्य लेते हुए उनका वर्गमूल ज्ञात करना, वर्ग माध्य मूल मान अर्थात Crms कहलाता है।

निष्कर्ष:-
1. यदि किन्हीं दो गैसों को समान अणुभार पर आपस में मिलाया जाये तो

2. यदि समान ताप पर, भिन्न -भिन्न अणुभार वाली गैसों को मिलाने पर –

विभिन्न गैस नियम तथा गैसों के अणुगतिक सिद्धान्त के आधार पर उनकी उत्पत्ति:-
गैस नियम
1. बॉयल का नियम (Boyle’s Law):- नियत ताप पर निश्चित द्रव्यमान वाली गैस का दाब उसके आयतन के व्युत्क्रमानुपाती होता है।
2. चार्ल्स का नियम (Charle’s law):- निश्चित द्रव्यमान वाली गैस का नियत दाब पर गैस का आयतन उसके परमताप T के समानुपाती होता है।
3. गैलुसेक का नियम (Gay – lussac’s law):- निश्चित द्रव्यमान वाली गैस के नियत आयतन पर गैस का दाब उसके परमताप के समानुपाती होता है।
आदर्श गैस समीकरण
- वह गैस जो सभी गैस नियमों की पालन करती हो, आदर्श गैस कहलाती है।
- आदर्श गैस के दाब, आयतन व ताप को एक गणितीय समी. में लिखना, आदर्श गैस समी. कहलाता है।
PV= nRT
आदर्श गैस नियतांक (R) का मान
- R = 8.314 Nmk-1mol-1
- R = 1.98 cal mol-1 k-1 (C.G.S)
गैस की औसत गतिज ऊर्जा :-
E = \(\frac{3RT}{2}\)
यह एक मोल गैस की औसत गतिज ऊर्जा कहलाती है। यह केवल गैस के परमताप पर निर्भर करती है, गैस की प्रकृति पर नहीं।
एक ग्राम गैस की औसत गतिज ऊर्जा
यह ताप व गैस की प्रकृति दोनों पर निर्भर करती है।
E = \(\frac{3}{2}\frac{RT}{M}\)
एक अणु की औसत गतिज ऊर्जा
Kb = 1.38 x 10-23 Jmol-1k-1
- Kb → बोल्टसमेन नियतांक
- यह गैस के परमताप पर निर्भर करती है।
आवोगाद्रो नियम
आवोगाद्रो के अनुसार समान ताप, दाब, आयतन की स्थितियों में गैसों में अणुओं की संख्या आपस में बराबर होती है।
ग्राहम के विसरण का नियम
ग्राहम के अनुसार गैस के विसरण की दर गैस के घनत्व के वर्गमूल के व्युत्क्रमानुपाती होती है।
Note :-
- गैसों के अणुओं का ताप बढने पर उनका वेग अर्थात् Crms का मान भी बढ़ने लगता है।
- गैसों का अणुगतिक सिद्धान्त मैक्सवेल व सेल्सियस ने दिया।
माध्य मुक्त पथ (Free Mean Path):-

गैसों के किन्हीं दो क्रमागत अणुओं के मध्य टक्कर के समय चली गयी कुल रेखीय दूरी मुक्त पथ कहलाती है। इन मुक्त पथों का N टक्करों के सापेक्ष लिया गया औसत, माध्य मुक्त पथ λ कहलाता है।
सूत्र (λ)
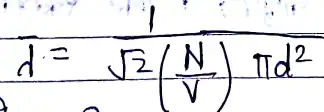
स्वतंत्रता की कोटियाँ (Degree of freedom):- किसी परमाणु की गति या उसकी स्थिति को दर्शाने के लिए जितने निर्देशांकों की या भौतिक राशियों की आवश्यकता होती है, उसकी स्वतंत्रता की कोटि कहलाती है।
Note
- दृढ़ पिण्ड के लिए स्वतंत्रता की कोटि का मान 6 होता है। जिसमें से तीन उसके रेखीय गति को दर्शाती है व शेष बची तीन घूर्णन गति को दर्शाती है।
- किसी भी परमाणु के लिए स्वतंत्रता की कोटि निम्न प्रकार से ज्ञात की जाती है :-
- F = 3N-K
- आकाश में उड़ते हुए वायुयान के लिए स्वतंत्रता की कोटि का मान 3 होता है।
(i) एक परमाण्विय गैस के लिए स्वतंत्रता की कोटि :-
एक परमाण्विय गैस का अर्थ यह है कि उसमें केवल एक ही परमाणु हो।
f = 3
(ii) द्विपरमाण्विय गैस के लिए स्वतंत्रता कोटि:-
द्विपरमाण्विय गैस का अर्थ यह है कि उसमें परमाणुओं की संख्या 2 हो ।
f = 5
(iii) त्रिपरमाण्विय गैस के लिए स्वतंत्रता कोटि :-
a. रेखीय संरचना
F= 7
b. त्रिभुजीय संरचना
f = 6
मैक्सवेल का ऊर्जा समविभाजन नियम
मैक्सवेल के अनुसार समान ताप की स्थिति में किसी भी निकाय के प्रत्येक स्वतन्त्रता की कोटि के लिए औसत गतिज ऊर्जा का मान एकसमान होता है। जोकि ½KT होता है। जहाँ K बोल्टजमेन नियतांक व T परमताप कहलाता है।
गैसों की मोलर विशिष्ट उष्माधारिताएँ :-
| परमाण्वियता | स्वतंत्रता की कोटि | एक अणु की औसत गतिज ऊर्जा | एक मोल की औ. ग. ऊर्जा [E] | Cv=(dE)/(dT) | CP=Cv+R | r=(Cp)/(Cv) |
|---|---|---|---|---|---|---|
| एक परमाण्वियता गैस | 3 | (3/2)KT | (3/2)RT | Cv=(3/2)R | CP=(3/2)R+R CP=(5/2)R | r={(5/2)R}/{(3/2)R} r=5/3 r=1.67 |
| द्वि परमाण्वियता गैस | 5 | (5/2)KT | (5/2)RT | Cv=(5/2)R | CP=7/2R | r=1.4 |
| त्रिपरमाण्वियता गैस | ||||||
| (i) रेखीय संरचना | 7 | (7/2)KT | (7/2)RT | Cv=(7/2)R | CP=(9/2)R | r=1.28 |
| (ii) त्रिभुजीय संरचना | 6 | (6/2)KT =3KT | 3RT | Cv=3R | CP=4R | r=1.33 |
Tagged with: class 11 physics chapter 13 ncert notes in hindi | Class 11 physics Chapter 13 Notes in Hindi | Kinetic Theory Notes in Hindi | physics chapter 11 class 13 notes in hindi | physics class 11 chapter 13 in hindi notes
