यहाँ हमने Class 11 Physics Chapter 3 Notes in Hindi दिये है। Class 11 Physics Chapter 3 Notes in Hindi आपको अध्याय को बेहतर ढंग से समझने में मदद करेंगे और आपकी परीक्षा की तैयारी में सहायक होंगे।
Class 11 Physics Chapter 3 Notes in Hindi सरल रेखा मे गति
महत्वपूर्ण पद:-
- स्थिति में समय के सापेक्ष परिवर्तन:- गति
- दूरी में समय के सापेक्ष परिवर्तन:- चाल
- विस्थापन में समय के सापेक्ष परिवर्तन:- वेग
गतिः- किसी कण / पिण्ड की वह स्थिति जहाँ उसकी स्थिति में समय के साथ सतत् परिवर्तन हो रहा हो, तो वह स्थिति गति कहलाती हैं।
स्थिति को दर्शाने हेतु आवश्यकता होती हैं – निर्देश तंत्र
गति के प्रकार:-
दिशा / विमा के आधार पर:-
- एक विमीय गति
- द्विविमीय गति
- त्रिविमीय गति
- अगर स्थिति परिवर्तन के दौरान तीनों अक्षों में से किसी एक अक्ष का परिवर्तन हो तो उसे एक विमीय गति कहते है।
- अगर किसी गतिशील कण की स्थिति परिवर्तन के दौरान तीनों अक्षों में से किन्हीं दो अक्षों में परिवर्तन हो तो उसे द्विविमीय गति कहते है ।
- अगर किसी गतिशील कण की स्थिति परिवर्तन के दौरान तीनों अक्षों में परिवर्तन हो तो उसे त्रिविमीय गति कहते है।
गति की प्रकृति:-
- स्थानान्तरीय गति
- घूर्णन गति
- दोलन / कंपन गति
स्थिति में परिवर्तन का माप, दूरी या विस्थापन कहलाता है।
दूरी व विस्थापन में समानता:-
- मात्रक एक समान (लंबाई)
- विमीय समीकरण एक समान [L] या [M0LT0]
दूरी व विस्थापन में असमानता:-
- वास्तविक पथ की लंबाई दूरी कहलाती है जबकि प्रारम्भिक एवं अंतिम स्थिति के बीच की न्यूनतम दूरी विस्थापन कहलाती है।
- दूरी सदैव धनात्मक होती है जबकि विस्थापन धनात्मक व ऋणात्मक दोनों हो सकता है।
- दूरी अदिश होती है जबकि विस्थापन सदिश होता है।
- विस्थापन <= दूरी, अर्थात विस्थापन या तो दूरी के बराबर या दूरी से कम होता है।
- दूरी व समय का अनुपात चाल कहलाती है जबकि विस्थापन व समय का अनुपात वेग कहलाता है।
चाल व वेग
चाल
एकांक समय में तय दूरी चाल कहलाती है।
चाल के प्रकार:-
- औसत चाल
- तात्क्षणिक चाल
(i) औसत चाल:- किसी वस्तु द्वारा तय किये गये पथ एवं लगे समय का अनुपात औसत चाल कहलाती है ।
औसत चाल का गणितिय सूत्र, औसत चाल = \(\frac{Δx}{Δt}\)
(ii) तात्क्षणिक चाल:- किसी विशेष क्षण पर किसी वस्तु की चाल तात्क्षणिक चाल कहलाती है।
तात्क्षणिक चाल = \(\frac{dx}{dt}\)
सामान्य अर्थ:- दूरी का समय के सापेक्ष अवकलन तात्क्षणिक चाल कहलाती है।
वेग
एकांक समय में तय विस्थापन, वेग कहलाता है। वेग के प्रकार:- (i) औसत वेग, (ii) तात्क्षणिक वेग ।
(i) औसत वेग:- किसी वस्तु द्वारा तय किये गये विस्थापन एवं लगे समय का अनुपात, औसत वेग कहलाता है।
(ii) तात्क्षणिक वेग:- किसी विशेष क्षण पर किसी वस्तु का वेग, तात्क्षणिक वेग कहलाता है।
वेग व चाल में अन्तर
| चाल | वेग |
|---|---|
| एकांक समय में तय दूरी, चाल कहलाती है। | एकांक समय में तय विस्थापन, वेग कहलाता है। |
| यह अदिश होती है। | यह सदिश होता है। |
| तयपथ की लम्बाई व लगे समय का अनुपात | कुल विस्थापन एवं विस्थापन में लगे समय का अनुपात। |
वेग व चाल में समानता
तात्क्षणिक वेग व तात्क्षणिक चाल एक समान होते है।
मात्रक व विमीय समीकरण एक समान होते है।
- मात्रक = m/s
- विमीय समीकरण= [ M0LT-1 ]
त्वरण
वेग में परिवर्तन की दर, त्वरण कहलाता है।
- वेग में परिवर्तन = v2-v1 = Δv
- समयान्तराल = t2-t1 = Δt
त्वरण के प्रकार –
- औसत त्वरण
- तात्क्षणिक त्वरण
(i) औसत त्वरण:- वेग में परिवर्तन / परिवर्तन में लगा समय
aqv = \(\frac{Δv}{Δt}\)
(ii) तात्क्षणिक त्वरण:- किसी विशेष क्षण वस्तु का त्वरण, तात्क्षणिक त्वरण कहलाता है।
a = \(\frac{dv}{Δt}\)
अर्थात् वेग का समय के सापेक्ष अवकलन, त्वरण कहलाता है।
विशेष:-

विस्थापन का द्वितीय अवकलन त्वरण कहलाता है।
- विस्थापन का प्रथम अवकलन वेग कहलाता है|
- विस्थापन का द्वितीय अवकलन त्वरण कहलाता है
- वेग का प्रथम अवकलन त्वरण कहलाता है।
\(\frac{dv}{dt}\) की विशेषता :-
- वेग में परिवर्तन की दर को दर्शाता है।
- त्वरण की दर्शाता है।
- इसका मान धनात्मक, शून्य (नियत वेग), ऋणात्मक (वेग कमी) हो सकता है।
- ऋणात्मक मान मंदन को दर्शाता है।
- v-t वक्र पर खींची गई स्पर्श रेखा के ढाल को दर्शाता है।
- विस्थापन के द्वितीय अवकलन को दर्शाता है।
विशेष:-
असमान गति की विशेषताएँ:-
- समान समयान्तरालों में विस्थापन अलग-अलग होता है।
- वेग का परिमाण या दिशा या दोनों समय के साथ परिवर्तनशील होते है।
- विस्थापन और समय वक्र का ढाल नियत नहीं रहता है।
Also Check:- Chapter 2: मात्रक और मापन
किसी पिण्ड /वस्तु की गति के सम्पूर्ण अध्ययन हेतु पद:-
- निर्देश तंत्र में स्थिति के निर्देशांक
- स्थिति सदिश (r) ज्ञात करना
- विस्थापन ज्ञात करना (स्थिति सदिश में परिवर्तन)
- वेग
- त्वरण
त्रिविमीय गति की व्याख्या
माना एक त्रिविमीय निर्देशतंत्र S जिसका मूल बिन्दू O(0,0,0) है। जहाँ वस्तु की प्रारम्भिक स्थिति A (x1, y1, z1) व t = 0 है। Δt सेकण्ड के बाद स्थिति बदलकर B (x2, y2, z2) हो जाती है।
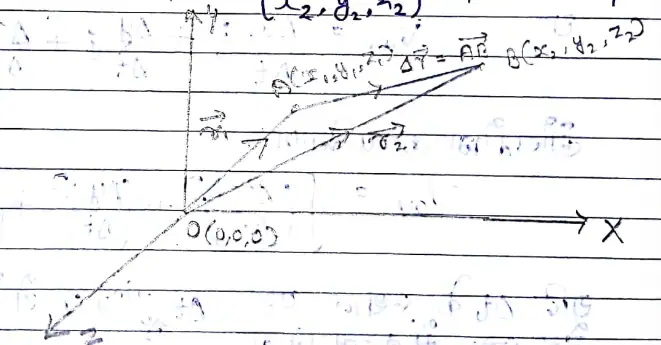
प्रथम स्थिति सदिश होगा

द्वितीय स्थिति सदिश
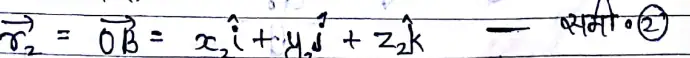
विस्थापन
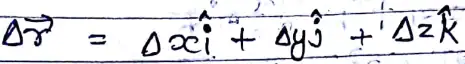
औसत वेग

त्वरण

द्विविमीय निर्देश तंत्र से
माना एक द्विविमीय निर्देश तंत्र S जिसका मूल बिन्दू O(0,0) है। जहाँ वस्तु की प्रारम्भिक स्थिति A (x1, y1) व t = 0 है। Δt सेकण्ड के बाद स्थिति बदलकर B (x2, y2) हो जाती है।

प्रथम स्थिति सदिश होगा

द्वितीय स्थिति सदिश होगा

विस्थापन

औसत वेग

त्वरण
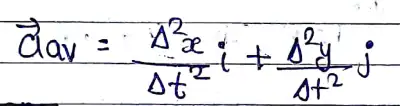
गति के प्रकार
सापेक्ष:- स्थिर बिन्दु या निर्देश तंत्र के प्रति किसी वस्तु की दूरी / विस्थापन में परिवर्तन की दर सापेक्ष गति / सापेक्ष वेग कहलाता है।
आपेक्षिक:- किसी गतिशील वस्तु / बिन्दु के सापेक्ष दूसरी / अन्य वस्तु की दूरी/विस्थापन में परिवर्तन की दर आपेक्षिक गति / आपेक्षिक वेग कहलाता है।
गुरुत्वीय बल
अगर किसी वस्तु को:-
- मुक्त अवस्था में पृथ्वी पर गिरने दे
- ऊपर की ओर एक निश्चित प्रारम्भिक वेग से फेंके
- न्यून कोण (0<θ<90) पर फेंके तो वस्तु की गति कैसी होगी ? व्याख्या कीजिए ।
उपरोक्त तीनों अवस्थाओं में वस्तु पर एक नियत मान का पृथ्वी द्वारा उत्पन्न आकर्षण बल कार्य करता है, जिसे गुरुत्वीय बल कहते है। जिसका मान होता है-
F = mg
m → वस्तु का द्रव्यमान
g→ गुरुत्वीय त्वरण
g का मान एक निश्चित ऊँचाई तक लगभग नियत रहता है। अत: वस्तु की गति समान त्वरित होगी।
अत: उपरोक्त गति में न्यूटन के तीनों गति समीकरण लागू होंगे।
न्यूटन गति समीकरण
(i) स्वतन्त्रतापूर्वक गिरती वस्तु के लिए :-

- V = gt
- S =1/2gt2
- v2 = 2gs
- v = √2gs
(ii) ऊर्ध्व दिशा में u वेग से फेंके तो t सेकण्ड बाद:-

- v=u-gt
- S = ut – \(\frac{1}{2}gt^2\)
- v2 = u2 – 2gs
iii) पृथ्वी तल के साथ , θ कोण पर वस्तु को u वेग से फेंके तो
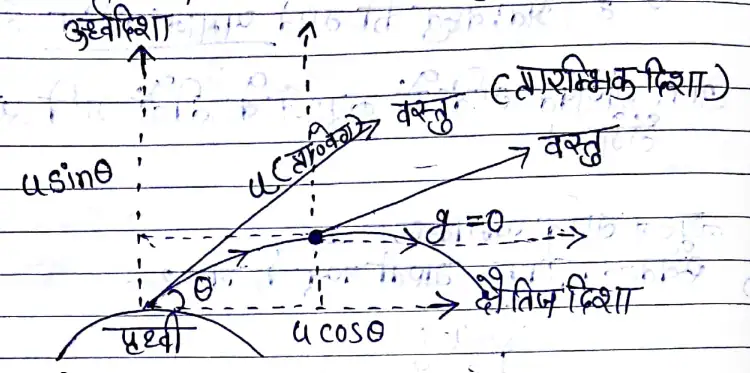
X-अक्ष (क्षैतिज दिशा में) के अनुदिश,
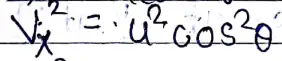
y- अक्ष, (ऊध्व दिशा में) अनुदिश
V2g = u2sin2θ – 2gy
परवलयकार गति / प्रक्षेप्य गति :-
अगर किसी वस्तु/पिंड को पृथ्वी धरातल के साथ न्यून कोण पर फेंका जाए तो वह हवा में तैरती हुई पुनः पृथ्वी पर लौट आती है। जिसका पथ परवलय आकार (अर्द्धचन्द्राकार) होता है, यह गति प्रक्षेप्य गति कहलाती है।
प्रक्षेप्य गति की विशेषताएँ:-
- पिंड/ वस्तु को न्यून कोण पर फेंका जाना चाहिए।
- गति का पथ परवलयकार होता है।
- गति में उत्पन्न त्वरण एकसमान होता है, जिसका मान गुरुत्वीय त्वरण (g) के तुल्य होता है। (9.8 or 10)
- गति समान त्वरित होती है।
- इसकी व्याख्या हेतु न्यूटन गति समीकरण उपयोगी होते है।
- यह द्विविमीय गति होती है। इसी कारण व्याख्या हेतु विस्थापन, वेग एवं त्वरण को दो घटकों में विभाजित करते हैं:-
- क्षैतिज घटक
- उध्र्व घटक
- पिंड / वस्तु जितने समय तक हवा में रहती है। वह समय उड्डयन काल कहलाता है।
- प्रारम्भिक व अन्तिम स्थितियों के बीच की सीधी दूरी गति के लिए परास (Range) कहलाती है।
- अधिकतम ऊँचाई पर वेग का उर्ध्व घटक शून्य होता है।
- अधिकतम ऊँचाई तक जाने में लगा समय वहाँ से गिरने में लगे समय के बराबर होता है।
अधिकतम ऊँचाई (H)
पृथ्वी तल से अधिकतम ऊंचाई वह होती है। जहाँ वेग का ऊर्ध्व घटक vy=0 होता है।

यहाँ ऊर्ध्व घटक के लिए V = 0 व u = u sinθ है।
अधिकतम ऊँचाई पर पहुँचने में लगा समय :-

उड्डयन काल (T)
जब तक पिण्ड हवा में रहता है या फेंकने से लेकर पुन: पृथ्वी पर टकराने में लगा समय।
उड्डयन काल (T) = 2 x अधिकतम ऊँचाई तक जाने में लगा समय
परास (R)
अंतिम स्थिति (पृथ्वी पर) व प्रारम्भिक स्थिति के बीच की सीधी दूरी (क्षैतिज दूरी), परास कहलाती है।

विशेष:-
अधिक परास हेतु Sin 2θ का मान अधिकतम (1) होना चाहिए।
अर्थात् Sin 2θ = 1
जब 2θ = 90
या θ =45
अधिकतम परास :- Rmax = \(\frac{u^2}{g}\)
θ के लिए परास Rθ = \(\frac{u^2sin2θ}{g}\)
θ के लिए परास R90-θ = \(\frac{u^2sin2θ}{g}\)
पथ समीकरण:- निर्देशांकों में सम्बन्ध दर्शाने वाला सूत्र पथ का समीकरण कहलाता है।
Class 11 Physics Chapter 3 Notes in Hindi PDF Download
Tagged with: class 11 physics chapter 3 ncert notes in hindi | Class 11 physics Chapter 3 Notes in Hindi | Motion in a Straight Line Notes in Hindi | physics chapter 3 class 11 notes in hindi | physics class 11 chapter 3 in hindi notes
what is physics