Class 11 Physics Chapter 10 Notes in Hindi तरल पदार्थों के यांत्रिक गुण

यहाँ हमने Class 11 Physics Chapter 10 Notes in Hindi दिये है। Class 11 Physics Chapter 10 Notes in Hindi आपको अध्याय को बेहतर ढंग से समझने में मदद करेंगे और आपकी परीक्षा की तैयारी में सहायक होंगे।

Class 11 Physics Chapter 10 Notes in Hindi तरल पदार्थों के यांत्रिक गुण

Definition (परिभाषा)

पदार्थ की वह अवस्था (द्रव+गैस) जिसमें बहाव का गुण या गतिशील हो।

बहाव की निर्भरता – दाबान्तर ।

द्रव व दाब में गहरा सम्बन्ध है :- द्रव पर दाब का प्रयोग करके वैज्ञानिको ने बड़ी-बड़ी समस्याओं का हल ढूँढ लिया।

दाब (Pressure)

एकांक क्षेत्रफल पर लगने वाला बल, दाब कहलाता है। 

P = \(\frac{F}{A}\)

• मात्रक – \(\frac{N}{m^2}\) या पास्कल
• विमीय समीकरण –  M¹L^-1T^-2 

P बढ़ाने का तरीका अगर F नियत रहे →  क्षेत्रफल को कम करके

दाब मापने का उपकरण:-  बेरोमीटर / दाबमापी 

• दाबमापी बनाने में तरल (विशेषकर द्रव) का प्रयोग किया जाता है।
• द्रव + गैस = तरल 

तरल के अन्दर स्थित किसी बिन्दु पर तरल द्वारा उत्पन्न दाब

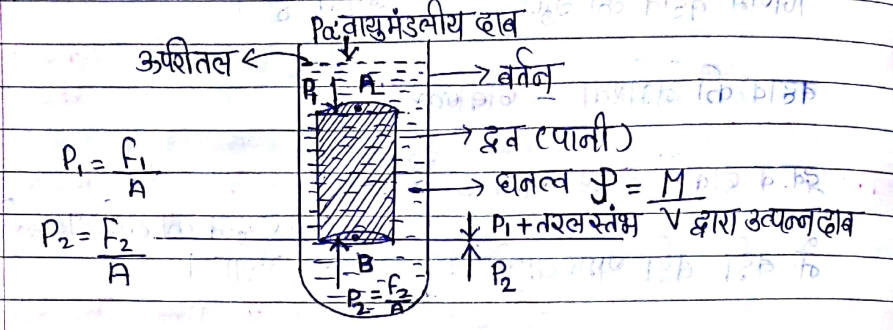
P2 = Pa + ρgh

पास्कल का नियम

अगर किसी तरल (द्रव या गैस) के ऊपर किसी भाग पर दाब लगाया जाए तो वह दाब पूरे तरल में सभी दिशाओं में एक समान मात्रा में संचरित होगा यही पास्कल का नियम है।

पास्कल नियम पर आधारित मशीनों के नाम:-

1. हाइड्रोलिक ब्रेक 
2. हाइड्रोलिक लिफ्ट जैसे:- क्रेन 

हाइड्रोलिक लिफ्ट :-

1. द्रव (तरल) से आंशिक रूप से भरा ऐसा बर्तन जिसके साथ दो अलग-अलग अनुप्रस्थ काट वाले पाइप जुड़े होते है।
2. दोनों पाइपों में पिस्टन P₁ व P₂ लगे हुए है।
3. किसी एक पिस्टन को दबाएँगे दूसरा उल्टी दिशा में गति करने लगेगा।
4. जिस वस्तु का वजन मापना हो या ऊपर उठाना हो, उसे P2 पिस्टन पर रख देंगे।

हाइड्रोलिक ब्रेक:-

हाइड्रोलिक ब्रेक में :-

1. तरल के रूप में Oil प्रयोग होता है जो Break Oil कहलाता है।
2. दो सिलिण्डर होते है – मास्टर व सामान्य, ये परस्पर नलियाँ (समान मोटाई की) द्वारा जुड़े होते है।
3. मास्टर सिलिण्डर का संबंध पेण्डल से होता है जबकि सामान्य सिलिण्डर का ब्रेक शू से।
4. पेण्डल द्वारा दाब उत्पन्न किया जाता है जो तरल के अंदर संचरित होकर ब्रेक शू को दबाएंगे फलस्वरूप टायर जाम हो जाते है |

वायुदाब

समुद्री तल पर पारे के स्तम्भ जिसकी ऊँचाई (76 cm) के द्वारा उत्पन्न दाब, वायुमण्डलीय दाब कहलाता है। जिसका

1 atm = 10 पास्कल या  10⁵ N/m²

तरल (Fluid)

बहाव गुण वाला कोई भी द्रव्य तरल (Fluid) कहलाता है।

कारण

तरल में अव्यवों (परमाणु/अणु) की व्यवस्था परतों के रूप में होती है। ये परतें एक-दूसरे पर फिसलने का गुण रखती है।

जैसे:-

जिस प्रकार ठोसों में बाह्य परिवर्तन का विरोध करने का गुण (जड़त्व) होता है उसी प्रकार तल की इन परतों के मध्य में बहाव के दौरान विरोधी गुण होता है; यह विरोधी गुण (श्यानता ) कहलाता है।

इस विरोध के कारण उत्पन्न बल ( विरोधी बल ), श्यान बल कहलाता है।

श्यान बल की व्याख्या (F_v):-

• परतों के मध्य उत्पन्न विरोधी बल (श्यान बल ), परतों के मध्य उत्पन्न आपेक्षिक वेग का विरोध करता है।
• परतों का वेग ऊर्ध्व दिशा में बढ़ता जाता है।
• सबसे नीचे स्थित परत का वेग न्यूनतम (लगभग शून्य) तथा सबसे ऊपरी परत का वेग अधिकतम होता है।
• वेग में ऊर्ध्व दूरी के साथ परिवर्तन की दर = \(\frac{dv}{dz}\) या \(\frac{v}{l}\)

F_v = -ηA\(\frac{dv}{dz}\)

• अतः श्यानता गुणांक η =\(\frac{F_v}{A\frac{dv}{dz}}\)
• इकाई = Nsm^-2
• विमीय समीकरण= ML^-1T^-1

η की परिभाषा:- एकांक सम्पर्कित क्षेत्रफल वाली परतों के मध्य वेग प्रवणता को एकांक बनाये रखने के लिए आवश्यक बल , श्यानता गुणांक कहलाता है।

Chapter 2: मात्रक और मापन
Chapter 3: सरल रेखा मे गति
Chapter 4: गति के नियम
Chapter 6: कार्य, शक्ति एवं ऊर्जा
Chapter 7: कणों के निकाय तथा घूर्णी गति
Chapter 14: दोलन गति

तरल प्रवाह स्वरूप

• धारा रेखीय प्रवाह [Stremline]- शांत, अनुशासित  
• विक्षुब्ध प्रवाह [Turbulent] – अशांत

प्रवाह का स्वरूप तरल के वेग पर निर्भर करता है। 

वेग वृद्धि के साथ प्रवाह स्वरूप बदलने लगता है। वेग के विशेष मान (Vc) पर प्रवाह विक्षुब्ध हो जाता है।

• अगर  (l)  V ≤ V_c धारा रेखीय रहेगा
• (II) V> V_c   विक्षुब्ध हो जाएगा

रेनाल्ड संख्या (R)

प्रवाह स्वरूप के निर्धारण हेतु वैज्ञानिकों ने एक विशेष भौतिक राशि को निर्धारित किया जो रेनाल्ड संख्या (R) कहलाती है।

R निम्न कारकों पर निर्भर करता है :-

• (i) पाइप की मोटाई (D)
• (ii) तरल का घनत्व (ρ)
• (iii) तरल का वेग (v)
• (iv) तरल की शयानता (η)

R =\(\frac{ρVD}{η}\)

• (i) R ≤ 1000 धारा रेखीय प्रवाह 
• (ii) R  ≥ 2000 विक्षुब्ध प्रवाह

तरल प्रवाह की दर

असमान अनुप्रस्थ काट वाला पाइप जिसमे कोई तरल (विशेषकर द्रव) बह रहा है, वेग व अनुप्रस्थ काट छेत्रफल का गुणनफल सदैव नियत रहता है।

तरल में गिरती ठोस वस्तु / पिण्ड का वेग

किसी वस्तु पर ( गिरते समय ) तरल में निम्न बल कार्य करते है:-

1. वस्तु का भार (गुरुत्वीय बल) ↓ F_g
2. तरल का श्यान बल ↑ (F_v)

• प्रारंभ में केवल गुरुत्वीय बल कार्य करेगा यानी वेग में वृद्धि होती जाएगी।
• एक समय / स्थिति पर इन बलों को योग गुरुत्वीय बल के तुल्य हो जाएगा, तब वेग वृद्धि रुक जाएगी तथा वस्तु एक नियत वेग से गिरने लगेगी। यह वेग सीमान्त वेग (टर्मिनल वेग) (Vt) कहलाता है।

बरनूली सिद्धान्त

“किसी असमान अनुप्रस्थ काट क्षेत्र वाले पाइप में धारा रेखीय गतिशील आदर्श द्रव (जिसका श्यान बल शून्य हो व असंपीडय) के एकांक आयतन के एकांक समय के लिए दाब ऊर्जा, गतिज ऊर्जा एवं स्थितिज ऊर्जाओं का योग सदैव नियत रहता है।”

दाब द्वारा किया गया कार्य +गतिज ऊर्जा द्वारा किया कार्य + स्थितिज ऊर्जा द्वारा किया गया = Constant

बरनूली सिद्धांत के अनुप्रयोग:-

• स्प्रै बरनूली सिद्धांत के अनुसार कार्य करता है।
• मेगनस प्रभाव (विशेषकर क्रिकेट की बाउन्स होना)
• हवाईजहाज का उड़ना या उतरना 
• वेन्ट्यूरी मापी:- बहते हुए द्रव की मात्रा ज्ञात करने वाला उपकरण जो बरनूली सिद्धांत पर कार्य करता है।
• पिटोट नली:- प्रवाहित द्रव का वेग ज्ञात करने का उपकरण जो बरनूली सिद्धांत पर आधारित है।

बहि: स्राव वेग:- किसी तरल से भरे बर्तन में कुछ गहराई (h) पर बने छिद्र में से निकलने वाले तरल का वेग बहि: स्त्राव वेग कहलाता है।

टॉरीसॉली सिद्धान्त:-समान गहराई व ऊँचाई से क्रमश: बने छिद्र में से निकले तरल व मुक्त रूप से गिरती किसी वस्तु का वेग एक समान होता है । यही सिद्धान्त टॉरीसॉली सिद्धांत कहलाता है |

पृष्ठ तनाव (Surface tension) 

• पृष्ठ तनाव तरल का एक विशेष गुण है।
• तरल के पृष्ठ पर स्थित अणुओं पर अंदर की ओर एक नेट बल कार्यरत होता है जबकि अन्य वस्तुओं पर यह बल = 0। यही बल पृष्ठ तनाव कहलाता है।

पृष्ठ तनाव का मान

किसी तरल के पृष्ठ पर खींची गयी काल्पनिक रेखा (L मीटर) के लंबवत् (पृष्ठ तल में स्थित) एकांक लंबाई पर लगने वाला बल (F) पृष्ठ तनाव कहलाता है।

• \(T=\frac{F}{L}\)
• S.I. मात्रक:-  न्यूटन प्रति मीटर = N/m
• विमीय समीकरण:- M¹L⁰T^-2
• तरल का वह गुण जिसके कारण तरल न्यूनतम पृष्ठ वाली आकृति ग्रहण करना चाहता है, पृष्ठ तनाव कहलाता है।
• चुकि पृष्ठ तनाव के कारण तरल हमेशा अपने न्यूनतम पृष्ठ को ग्रहण करना चाहता है। अत: तरल के पृष्ठीय क्षेत्रफल में एकांक परिवर्तन हेतु तरल द्वारा किया गया कार्य पृष्ठ तनाव कहलाता है।
• यानी T = \(\frac{w}{ΔΑ}\)
• S.I. मात्रक:- J/m²
• विमीय समीकरण:-  M¹L⁰T^-2

द्रव बूँद का निर्माण तथा इस पर कार्यरत बल

द्रव बूँद बनने का मुख्य कारण = पृष्ठ तनाव 

1. बूँद के पृष्ठीय क्षेत्रफल को कम करेगा = पृष्ठ तनाव के कारण उत्पन्न बल
2. बूँद के पृष्ठीय क्षेत्रफल को बढाएगा = द्रव बूँद के अन्दर का दाब जो बाह्य दाब से अधिक है

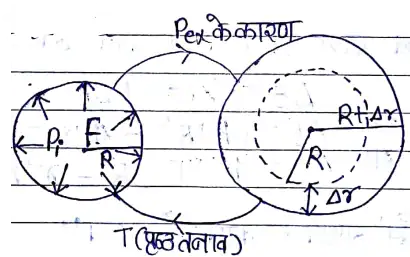
P_ex = \(\frac{2T}{R}\) यही पृष्ठ तनाव का दावाधिक्य में संबंध है।

विशेष :-

• उपरोक्त संबंध तभी उपयोगी होगा जब बूँद में एक तरफ हवा हो । जैसे- जल बूँद या वर्षा की बूँद । 
  • जल के अन्दर बना वायु का बुलबुला P_ex = \(\frac{2T}{R}\)
• परन्तु वायु से बना bubble (यदी बूंद खोखली है तो इसमें दो पृष्ठ होगें) जहाँ अंदर व बाहर दोनों ओर वायु होती है, के लिए उपरोक्त संबंध हो जाएगा। P_ex = \(\frac{4T}{R}\)

तरल या ठोस पदार्थों के अणुओं के या परमाणुओं को परस्पर बांधकर रखने वाला बल :- अन्त: परमाण्विक बल या अन्त: आण्विक बल 

• इनकी प्रकृति विद्युत चुंबकीय बल की होती है। 
• साम्यावस्था दूरी = 10^-9 मीटर

• अगर अणुओं के बीच की दूरी 10^-9m से कम हो तो:- प्रतिकर्षण 
• अगर अणुओं के बीच की दूरी 10^-9m से अधिक हो तो:- आकर्षण

अन्तः आण्विक बलों के प्रकार :-

1. ससंजक बल 
2. आसंजक बल

1. ससंजक बल:- ” एक ही प्रकार के द्रव या तरल के अणुओं के मध्य लगने वाला बल, ससंजक बल कहलाता है।”

 जैसे:- जल के अणुओं के मध्य लगने वाला बल, पारे के अणुओं के मध्य लगने वाला बल ।

2. आसंजक बल:- “दो भिन्न द्रवों के अणुओं के मध्य लगने वाला बल, आसंजक बल कहलाता है।”

जैसे :- जल व कांच के अणुओं के मध्य, पारे व जल के अणुओं के मध्य ।

तरल (Fluid)

मेनिस्कस व संपर्क (स्पर्श) कोण:-

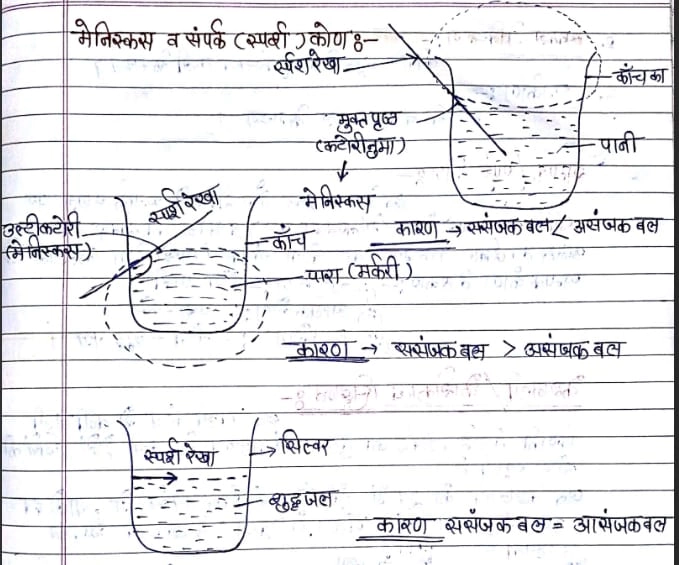
परिभाषा:– किसी भी द्रव से भरे बर्तन में द्रव के मुक्त पृष्ठ की आकृति वक्राकार होती है। अगर संसजक बल व आसंजक बल असमान हो, यह वक्राकार आकृति मेनिस्कस कहलाती है।

मेनिस्किस के प्रकार:-

• उत्तल –  ससंजक बल > आसंजक बल 
• अवतल – ससंजक बल <आसंजक बल

1. उत्तल मेनिस्कस:- कोण – अधिक कोण (काँच व पारे के बर्तन के मध्य)
2. अवतल मे निस्कस:- कोण – न्यून कोण (काँच व पानी के मध्य)
3. समकोण:- चाँदी व शुद्ध जल के मध्य ।

सम्पर्क / स्पर्श कोण:-

द्रव के मुक्त पृष्ठ और दीवार के सम्पर्क स्थल पर खींची गई स्पर्श रेखा (मेनिस्कस पर) व बर्तन की दीवार (द्रव के अन्दर की दीवार) के मध्य बना कोण संपर्क / स्पर्श कोण कहलाता है।

सम्पर्क कोण के प्रकार:-

1. न्यून कोण:- काँच-पानी
2. अधिक कोण:- पारा-काँच
3. समकोण :- चाँदी-शुद्धजल ।

केशनली/केशिकात्व सिद्धान्त

एक पतली काँच से बनी नली जिसकी मोटाई, लंबाई की तुलना में नगण्य हो तथा दोनों सिरों की ओर खुली हो।

जब केशनली को द्रव में डुबोते है (आंशिक रूप से) तो, या तो द्रव ऊपर चढ़ेगा या नीचे गिरेगा, ये क्रिया केशिकात्व सिद्धान्त कहलाती है।

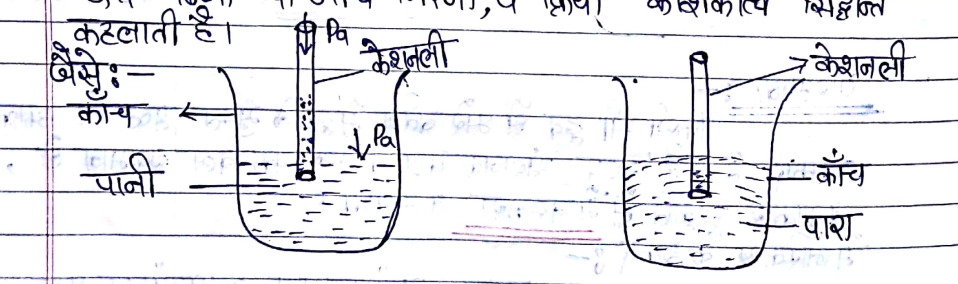
कारण:-  मेनिस्कस से उत्पन्न दाबान्तर।

इस दाबान्तर को सन्तुलित करने हेतु केशनली में द्रव ऊपर चढ़ता या नीचे उतरता है।

दैनिक जीवन में केशिकात्व का उपयोग:-

1. किसी चिमनी में केरोसीन का बत्ती से ऊपर चढना।
2. पत्तियों तक तने के माध्यम से पानी का पहुँचना।
3. तौलिये से गीले शरीर को पोंछना।
4. स्याही सोंखने वाले पेपर द्वारा स्याही का सोखना।

अपमार्जक:-  अपमार्जक वे पदार्थ जो पानी में मिलकर पानी के पृष्ठ तनाव को कम करते हैं। जिससे कपड़े पर लगे धब्बे आसानी से साफ हो जाते है।

पृष्ठ तनाव को प्रभावित करने वाले कारक:-

• 1. तापमान:- किसी भी लिक्विड /द्रव का तापमान बढाने पर उसका पृष्ठ तनाव कम होगा।
• अशुद्धि मिलाने पर:-  किसी द्रव में अघुलनशील पदार्थ को मिलाने पर पृष्ठ तनाव के मान में कमी आती है।

जैसे:- तेल, केरोसीन, घास-फूस आदि।

जबकि किसी द्रव में घुलनशील पदार्थ मिलाने पर उसके पृष्ठ तनाव के मान में वृद्धि होती है। जैसे:- चिनी मिलाने पर।

Tagged with: class 11 physics chapter 10 ncert notes in hindi | Class 11 physics Chapter 10 Notes in Hindi | Mechanical Properties of Fluids Notes in Hindi | physics chapter 10 class 11 notes in hindi | physics class 11 chapter 10 in hindi notes