Physics Class 12 Chapter 2 Notes in Hindi
स्थिर विद्युतविभव:- एकांक आवेश का अनंत से विद्युत क्षेत्र भीतर किसी बिंदु P तक लाने में किए गए कार्य को उस बिंदु पर विभव (electric potential in Hindi) कहते हैं। इसे V से सूचित करते हैं। विद्युत विभव का मात्रक जूल/कूलाम अथवा वोल्ट होता है। विद्युत विभव एक अदिश राशि है।
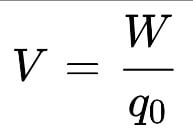
बिंदु आवेश के कारण विभव:-
यदि बिन्दु आवेश ( + Q ) बिन्दु O पर स्थित है । बिन्दु आवेश ( + Q ) से r दूरी पर स्थित बिन्दु P पर विद्युत क्षेत्र की तीव्रता ज्ञात करने के लिए बिन्दु P ( प्रेक्षण बिन्दु ) पर एक परीक्षण आवेश ( +q₀ ) रखते हैं ।
विद्युत द्विध्रुव के कारण विभव:–
परिमाण में समान किन्तु प्रकृति में विपरीत जब दो आवेश निम्न दूरी पर रखे हो तो ऐसे समूह को विद्युत द्विध्रुव कहते है।
विद्युत द्विध्रुव के कारण विद्युत विभव का मान ज्ञात करेंगे की द्विध्रुव के कारण किसी बिंदु पर उत्पन्न विभव का मान कितना होता है।
- माना आवेश -q तथा +q अल्प दुरी पर रखे है , इस द्विध्रुव को AB से चित्र में प्रदर्शित किया गया है तथा दोनों आवेशों के मध्य की अल्प दूरी को 2r माना गया है।
- हम इस द्विध्रुव युग्म के कारण बिन्दु P पर विद्युत विभव का मान ज्ञात करेंगे। ध्रुव के मध्य बिंदु अर्थात केंद्र बिंदु को O से दर्शाया गया है , द्विध्रुव अक्ष से OP θ कोण बना रहा है।
- माना OP की दूरी r , AP की दूरी r1 तथा BP के मध्य की दूरी r2 है।
- P बिंदु पर A बिन्दु पर स्थित -q आवेश के कारण उत्पन्न विद्युत विभव का मान
- इसी प्रकार B बिन्दु पर स्थित +q आवेश के कारण P बिंदु पर उत्पन्न विद्युत विभव का मान
- P बिंदु पर +q तथा -q आवेश के कारण उत्पन्न कुल विभव का मान
V = V1 + V2
आवेशों के निकाय के कारण विद्युत विभव
आवेशों के निकाय के कारण विद्युत क्षेत्र की तीव्रता सभी आवेशों के कारण उत्पन्न विद्युत क्षेत्र के सदिश योग के बराबर होता है। लेकिन विद्युत विभव अदिश राशि है अतः किसी बिंदु पर विद्युत विभव का मान सभी आवेशों के कारण अलग अलग उत्पन्न विद्युत विभव के अदिश योग के बराबर होता है।
अर्थात यदि किसी बिंदु पर आवेशों के निकाय के कारण विद्युत विभव ज्ञात करना है तो उस बिंदु पर सभी आवेशों के कारण अलग अलग विभव का मान ज्ञात करेंगे और उसके बाद सभी का अदिश योग करने से उस बिंदु पर सभी आवेशों के निकाय के कारण विद्युत विभव का मान प्राप्त होता है।
आवेशों के द्वारा उत्पन्न विद्युत क्षेत्र में एक बिंदु P है , P बिंदु पर हमें इन n आवेशों के कारण विद्युत विभव का मान ज्ञात करना है , P से आवेशों q1 , q2 , q3 …qn के मध्य की दुरी क्रमशः r1 , r2 , r3 ….rn है।
तो P बिंदु पर अलग अलग आवेशों के कारण उत्पन्न विद्युत विभव का मान सभी आवेशों के कारण उत्पन्न विभव के बीजगणितीय योग के बराबर होगा। कुल विभव (V) = V1 + V2 + V3 …. +Vn
समविभव पृष्ठ
किसी वैद्युत क्षेत्र में खींचा गया वह पृष्ठ जिस पर स्थित सभी बिन्दुओं पर वैद्युत विभव बराबर हों, समविभव पृष्ठ कहलाता है। समविभव पृष्ठ पर किन्हीं दो बिन्दुओं के बीच वैद्युत विभवान्तर शून्य होता है। अत: किसी आवेश को समविभव पृष्ठ के एक बिन्दु से दूसरे बिन्दु तक ले जाने में कोई कार्य नहीं करना पड़ेगा। परन्तु यह तभी सम्भव है जबकि वैद्युत आवेश को वैद्युत क्षेत्र के लम्बवत् ले जाया जाये।
समविभव पृष्ठ प्रत्येक बिन्दु पर वैद्युत क्षेत्र की दिशा के लम्बवत् होता है। वैद्युत क्षेत्र में भिन्न-भिन्न बिन्दुओं पर क्षेत्र की दिशा बल-रेखाओं द्वारा प्रदर्शित की जाती है।
एक बिन्दु-आवेश + q से चलने वाली बल-रेखाएँ खींची गई हैं। बिन्दु-आवेश को केन्द्र मानकर खींचे गये किसी गोलीय पृष्ठ (spherical surface) का प्रत्येक बिन्दु, आवेश से समान दूरी पर होने के कारण समान वैद्युत विभव पर होगा। अत: इस प्रकार का गोलीय पृष्ठ समविभव पृष्ठ होगा। बिन्दु-आवेश से चलने वाली बल-रेखाएँ त्रिज्य (radial) होंगी तथा गोलीय पृष्ठ पर लम्बवत् होंगी।
आवेशों के निकाय की स्थितिज ऊर्जा
जब दो या दो से अधिक आवेशों को अनंत से लाकर एक दूसरे के समीप व्यवस्थित करके या रखकर एक निकाय बनाया जाता है , इस निकाय को बनाने के लिए एक कार्य करना पड़ता है और यह किया गया कार्य इस निकाय में स्थितिज ऊर्जा के रूप में संचित हो जाता है , इस संचित ऊर्जा को निकाय की स्थितिज ऊर्जा कहते है। इसको U से व्यक्त किया जाता है।
बाह्य क्षेत्र में स्थितिज ऊर्जा
1. एकल आवेश की स्थितिज ऊर्जा:- एकल आवेश की स्थितिज ऊर्जा अनन्त से लाने में लिए गए कार्य के समान होती है यह कार्य स्थितिज ऊर्जा के रूप में संचित हो जाता है ।
किसी बिंदु पर विद्युत छेत्र की तीव्रता E एकांक धनावेश पर कार्यरत बल का में होता है । तथा विद्युत विभव एकांक धनावेश को अनन्त से उस स्थिति तक लाने में किए गए कार्य के समान होता है ।
यदि किसी बिंदु जिसका स्थिति सदीश r है तो इस बिंदु पर एकल आवेश q की ऊर्जा
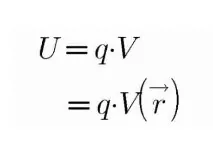
2. किसी बाह्य क्षेत्र में दो आवेशो के निकाय के बीच स्थितिज ऊर्जा :- इसमें हम दो आवेशों पर अध्ययन करेंगे , इन दोनों आवेशों को अनंत से लाकर एक निकाय की रचना करके इसकी स्थितिज ऊर्जा ज्ञात करेंगे।
माना दो आवेश है q1 तथा q2 , दोनों आवेश r दूरी पर रखे है , दोनों आवेशों की स्थिति क्रमशः A व B है अर्थात बिंदु A व B पर रखे है।
Q1 आवेश के कारण B पर उत्पन्न विद्युत विभव का मान
q1 तथा q2 दोनों आवेशों द्वारा रचित इस निकाय की विद्युत ऊर्जा
U = W = V1q2
यहाँ V1 का मान रखने पर
स्थितिज ऊर्जा = U
3.बाह्य क्षेत्र में विद्युत द्विध्रुव की स्थितिज ऊर्जा:– जब किसी विद्युत द्विध्रुव को अनंत से एक समान विद्युत क्षेत्र के समांतर लाया जाता है तो जितना कार्य आवेश को हराने में किया जाता है उतना ही कार्य आदेश के द्वारा प्राप्त हो जाता है क्योंकि आवेश द्वारा दूरी अधिक तय करनी पड़ती है इसीलिए ही आदेश पर विद्युत क्षेत्र द्वारा किया गया कार्य आदेश पर विद्युत क्षेत्र द्वारा किए गए कार्य से अधिक होता है।
चालक-स्थिरवैद्युतिकी
धातुओं के बाहर कक्ष में उपस्थित इलेक्ट्रॉनो को संयोजी इलेक्ट्रॉन कहते है जो धातु के अंदर गति करने के लिए स्वतंत्र होते है परन्तु धातु से मुक्त नहीं हो सकते है। धात्विक चालकों में ये वाहक इलेक्ट्रॉन होते हैं।
- किसी चालक के भीतर स्थिर विद्युत क्षेत्र शून्य होता है– प्रत्येक चालक में मुक्त इलेक्ट्रॉन होते है स्थितिक स्थिति में जब चालक के भीतर या पृष्ठ पर कोई विद्युत धारा नहीं होती है तब चालक के भीतर प्रत्येक स्थान पर विद्युत क्षेत्र शून्य हो होता है ।
- आवैशित चालक के पृष्ठ पर पृष्ठ के प्रत्येक बिंदु पर स्थिर विद्युत क्षेत्र अभिलंवबत होते है:- यदि विद्युत क्षेत्र पृष्ठ के अभिलम्ब नहीं है तो पृष्ठ के अनुदिश कोई शुन्यतर घटक होगा तथा पृष्ठ में मुक्त इलेक्ट्रॉन गति करना शुरू कर देंगे। अतः आवेशित चालक के पृष्ठ के प्रत्येक बिंदु पर स्थिर विद्युत क्षेत्र पृष्ठ के अभिलंवबत होना चाहिए ।
- स्थितिकी स्थिति में चालक के अभंतर कोई अतिरिक्त आवेश नहीं हो सकता :- जब किसी चालक के अंदर को आयतन अवयव लेते है तो दिया विद्युत आवेश केवल उस आयतन में नहीं होता तथा इससे गुजरने वाला कुल फ्लक्स शून्य होता है ।
- चालक के समस्त आयतन में स्थिर विद्युत विभव नियत रहता है तथा इसका मान इसके पृष्ठ पर एक समान होता है:- किसी चालक के अंदर विद्युत क्षेत्र शून्य होता है तथा इसके पृष्ठ पर कोई सतत् रेखीय घटक नहीं होता है। चालक के पृष्ठ पर या भीतर किसी आवेश को गति करने पर कोई कार्य नहीं होता है।
- आवेशित चालक के पृष्ठ पर विद्युत क्षेत्र:- किसी पृष्ठ पर आवेश घनत्व σ हो तो विद्युत क्षेत्र का मान इस स्थिति में पृष्ठ के अंदर स्थिर विद्युत क्षेत्र शून्य तथा बाहर विद्युत क्षेत्र पृष्ठ के अभिलम्बवत है अर्थात σ का मान शून्य से बड़ा होने पर विद्युत पृष्ठ के बर्हिमुखी अभिलम्बवत होगा।
स्थिर विद्युत परीक्षण
चालकों के अंदर विद्युत क्षेत्र शून्य होता है इस गुण का उपयोग स्थिर विद्युत परिक्षण हेतु सुग्रही उपकरणों को खोखले धातु के कोश में रखा जाता है।
जैसे :- तूफान के समय तड़ित विद्युत से बचने के लिए किसी कार के अंदर रहना पेड़ के नीचे खड़े होने से अधिक सुरक्षित है ऐसे खोखले चालकों को फैराडे पिंजरा कहा जाता है।
इसी सिद्धांत के आधार पर T V केवल को बनाया जाता है जिससे भूसंपर्कित धातु की जाली के अंदर से उच्च आवृत्ति की विद्युत तरंगों को प्रवाहित करते है।
परावैद्युत तथा ध्रुवण
परावैद्युत अचालक पदार्थ होते हैं। चालकों की तुलना में इनमें कोई आवेश वाहक नहीं होता। क्या होता है जब किसी चालक को किसी बाह्य विद्युत क्षेत्र में रखा जाता है? चालक में मुक्त आवेश वाहक गति करके अपने को इस प्रकार समायोजित कर लेते हैं |कि प्रेरित आवेशों के कारण विद्युत क्षेत्र बाह्य क्षेत्र का विरोध करता है।
यह उस समय तक होता रहता है जब तक कि स्थिर स्थिति में दोनों क्षेत्र एक-दूसरे का निरसन कर देते हैं तथा चालक के भीतर नेट स्थिरवैद्युत क्षेत्र शून्य होता है। किसी परावैद्युत में आवेश की यह मुक्त ।
गति संभव नहीं होती। फिर भी यह पाया जाता है कि बाह्य क्षेत्र परावैद्युत के पृष्ठ पर कुछ आवेश प्रेरित कर देता है जो एक ऐसा क्षेत्र उत्पन्न करता है जो बाह्य क्षेत्र का विरोध करता है। परंतु चालक से किसी बाह्य विद्युत क्षेत्र में किसी चालक तथा निरक्षित नहीं करता। यह केवल क्षेत्र को घटा देता है। इस प्रभाव की परावैद्युत के व्यवहार में अंतर। सीमा परावैद्युत की प्रकृति पर निर्भर करती है।
किसी पदार्थ के अणु ध्रुवी अथवा अध्रुवी हो सकते हैं। किसी अध्रुवी अणु में धनावेश तथा ऋणावेश के केंद्र संपाती अधवी अण| H. होते हैं। तब अणु का कोई स्थायी (अथवा आंतरिक) द्विध्रुव आघूर्ण नहीं होता। ऑक्सीजन (O) तथा हाइड्रोजन (H.) अणु अध्रुवी अणुओं के उदाहरण हैं।
संधारित्र तथा धारिता
संधारित्र:- एक ऐसी युक्ति जिसमें किसी चालक के आकार में परिवर्तन किए बिना उस पर आवेश की पर्याप्त मात्रा संचित की जा सकती है ऐसी युक्ति को संधारित्र (capacitor ) कहते हैं।
अथवा संधारित ऐसी दो चालकों का युग्म है जिस पर बराबर तथा विपरीत आवेश होता है।
संधारित्र की धारिता:- किसी संधारित्र की एक प्लेट को दिए गए आवेश तथा दोनों प्लेटों के बीच उत्पन्न विभवांतर के अनुपात को संधारित्र की धारिता कहते हैं। यदि किसी संधारित्र की प्लेट को +q आवेश देने पर उसकी प्लेटों के बीच V विभवांतर उत्पन्न होता है। तो संधारित्र की धारिता की परिभाषा से
C= q/ V
C को संधारित्र की धारिता कहते हैं। इसका मात्रक फैरड होती है।
समांतर पट्टिका संधारित्र
समांतर प्लेट संधारित्र में दो प्लेट कम दूरी पर व्यवस्थित करते है इन दोनों प्लेटों का आकार समान होना चाहिए।
ये दोनों प्लेट समान्तर व्यवस्थित होती है और एक संधारित्र की रचना करती है इसलिए इसे समान्तर प्लेट संधारित्र कहते है।
प्लेटो को आवेशित करने के लिए एक प्लेट को बैटरी के धन सिरे से तथा दूसरी प्लेट को बैट्री के ऋण सिरे से जोड़ते है।
जो प्लेट धन सिरे से जुडी है वह इलेक्ट्रॉन त्यागकर धनावेशित हो जाती है तथा जो प्लेट ऋण सिरे से जुडी है वह इलेक्ट्रॉन ग्रहण करके ऋणावेशित हो जाती है।
E = q/Kε0
धारिता पर परावैद्युत के प्रभाव
परावैद्युत माध्यम की उपस्थिति में धारिता के मान के वृद्धि हो जाती है। लेकिन यह वृद्धि इस बात पर निर्भर करती है कि प्लेटों के मध्य का भाग परावैद्युत पदार्थ से पूर्णतः आंशिक या विभिन्न परतों के रूप में किस प्रकार भरा हुआ है।
संधारित्र का संयोजन
धारिता में परिवर्तन करने के लिए दो अधिक संधारित्रों को एक साथ जोड़ने की आवश्यकता पड़ती है। संधारित्रों को जोड़ने के दो प्रमुख क्रम हैं।
1. श्रेणी क्रम संयोजन
2. समांतर क्रम संयोजन
- संधारित्र का श्रेणी क्रम संयोजन:- श्रेणी क्रम संयोजन के अंतर्गत पहले संधारित्र की दूसरी प्लेट को दूसरे संधारित्र की पहली प्लेट से जोड़कर तथा दूसरे संधारित्र की दूसरी प्लेट को तीसरे संधारित्र की पहली प्लेट से जोड़ देते हैं। ओर यदि संधारित्र की संख्या अधिक है तो आगे भी इसी क्रम में जोड़ते हैं। संधारित्र के इस संयोजन को श्रेणीक्रम संयोजन कहते हैं।
V = V1 + V2 + V3
2.संधारित्र का समांतर क्रम संयोजन:- समांतर क्रम संयोजन में दो या दो से अधिक संधारित्र को एक साथ जोड़ने के लिए प्रत्येक संधारित्र की पहली प्लेट को एक बिंदु X से जोड़ देते हैं। तथा प्रत्येक संधारित्र की दूसरी प्लेट को दूसरे बिंदु Y से जोड़ देते हैं। ओर यदि अधिक संधारित्र हैं। तो आगे भी इसी क्रम में जोड़ते हैं। तब संधारित्रों के इस संयोजन को समांतर क्रम संयोजन कहते हैं।
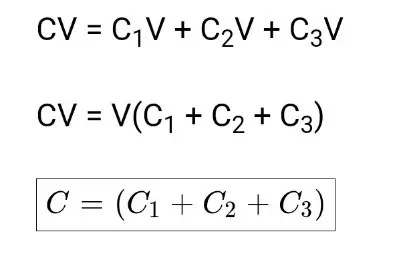
इसे भी पढे – Physics Class 12 Chapter 3 Notes in Hindi
संधारित्र में संचित ऊर्जा
किसी संधारित्र को उसके विद्युत क्षेत्र में आवेशित करने के लिए किया गया कार्य उस चालक की स्थतिज ऊर्जा या उसमें संचित ऊर्जा कहलाती है। यदि किसी संधारित्र की धारिता C हो तथा उसे q आवेश देने पर उसका विभव V हो तब V = q/c संधारित्र को सूक्ष्म आवेश dq देने में किया गया कार्य।
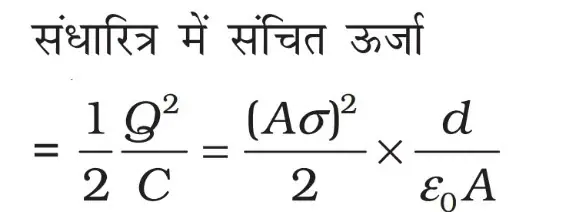
Tagged with: Class 12 Notes in Hindi | Class 12 Physics Chapter 2 Notes in Hindi | Class 12 physics Chapter 2 Notes in Hindi pdf | Physics Class 12 Chapter 2 Notes in Hindi | physics notes in Hindi