Summation notation is like a tool that adds up a bunch of numbers together. It uses the Greek letter Σ (Sigma) to denote the summation. This is especially helpful when dealing with a very long sum of terms that follow a particular pattern. Numerous branches of mathematics and statistics use summation notation.
The definition of summation notation and its mathematical representation will be covered in this article. We will learn how to express a lengthy sum of a sequence as summation notation. We will also give some examples to help you understand better
Definition of Summation Notation
Summation notation is used to represent the sum of a sequence of numbers. It provides a concise way to express the addition of multiple terms without writing them separately. It simplifies complex computations and makes mathematical expressions more manageable and readable.
The general form of summation notation is as follows:

Where;
- Σ indicates that we are adding up a series of terms.
- i is called the index of summation. It represents the place of the term in the series.
- i = 1 is the starting value of the index variable.
- n represents the upper limit of the index. It signifies how many terms there are in the series.
- xi is a function that defines the terms to be added together. The subscript i indicates the position of the term in the series.
Steps to Write Summation Notation
You can express the sum of a series of numbers in summation notation by following these steps:
- Understand the Pattern: Look at the numbers given in the sequence and understand the pattern.
- Select index variable: Choose an index variable to represent the position of each number in the sequence.
- Find the Start and End Limit: Find out where the sequence begins and ends.
- Use the Sigma Sign: Write down the Greek letter sigma Σ. Write the starting number below it and the ending number above the sigma symbol. Use your chosen index variable to show which numbers you are adding.
Steps for Expanding Summation Notation
The steps for extending summation notation are as follows:
- Substitute the index variable with its specific values from the range. Replace it first with the starting value. Then the next value, and so on until you reach the ending value.
- Write a positive symbol between each of the terms derived from the previous step.
You can also use a sigma calculator to expand the summation notation and find the sum with step-by-step solutions in no time.
Summation Notation Properties
- Summing the constant c nth times can be written as;

- Sum or difference of two sequences can be separated into the sum or difference of their individual parts.
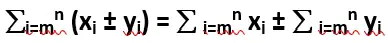
- Product and division of two sequences cannot be separated into their individual parts.
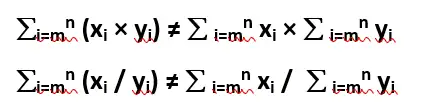
- A constant k can be factored out of the sum:

Summation Notation Formulas

Solve Examples
Example 1
Write the sum of the first 5 even numbers in summation notation.
Solution:
Step 1: Understand the Pattern
2, 4, 6, 8, and 10 are even numbers. The pattern is that each number is obtained by adding 2 to the previous number.
Step 2: Select Index Variable
Let us use the index variable i to represent the place of each number in the sequence.
Step 3: Find the Start and End limit
The sequence begins with the first even number, which is 2. Ends with the fifth even number that is 10.
Step 4: Use the Sigma Sign
Now we will use the Greek letter sigma Σ to represent the sum and apply the index variable i to show which numbers we are adding.

Example 2
Expand the following summation notation:

Solution:
Step 1: Substitute Index Values
Substitute the index variable i with its specific values from the range that is 2 to 4.
Substitute i = 2:
= 2(2) + 1 = 5
Substitute i = 3:
= 2(3) + 1 = 7
Substitute i = 4:
= 2(4) + 1 = 9
Step 2: Insert Plus Symbols
Insert a plus symbol between each of the terms obtained in the previous step.
= 5 + 7 + 9
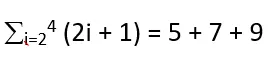
Summation Notation Applications
Some notable applications of summation notation are given below.
- Combinatory and Discrete Mathematics: Summation notation finds applications in combinatory, graph theory, and number theory. It helps solve problems related to permutations, combinations, and discrete structures.
- In calculus: Summation notation helps to define Riemann sums, integrals, and derivatives. This notation simplifies the process of finding the total area or accumulated value by summing infinitesimally small contributions.
- Sequence and Series: Summation notation is widely used to represent arithmetic, geometric, and other types of series. It helps describe patterns in sequences and provides a compact representation for summing a large number of terms.
- In statistics and probability: summation notation is used to represent probabilities, expected values, and other statistical measures
Conclusion:
In this article, we have explained the definition of summation notation. We looked at the steps of writing and expanding summation notation. We covered its applications to explore its significance. We have provided some solved examples of writing summation notation.
Tagged with: Summation Notation | Summation Notation Example
