यहाँ हमने Class 11 Physics Chapter 1 Notes in Hindi दिये है। Class 11 Physics Chapter 1 Notes in Hindi आपको अध्याय को बेहतर ढंग से समझने में मदद करेंगे और आपकी परीक्षा की तैयारी में सहायक होंगे।
Class 11 Physics Chapter 1 Notes in Hindi मात्रक और मापन
भौतिक राशि:- हमारे आस-पास बहुत सी वस्तुएँ पाई जाती हैं। प्रत्येक वस्तु का कोई न कोई गुण होता । यदि इस गुण का मापन किया जा सके तो यह गुण भौतिक राशि कहलाती है।
भौतिक राशियों को दो भागों में बाँटा गया है-
- मूल राशियाँ
- व्युत्पन्न राशियाँ
मूल राशियाँ (Fundamental Quantities)
वे भौतिक राशियाँ जो किसी अन्य भौतिक राशियो पर निर्भर नहीं करती है मूल राशियाँ कहलाती है।
ये कुल सात प्रकार की होती हैं:-
- लम्बाइ
- द्रव्यमान
- समय
- ताप
- विद्युत धारा
- पदार्थ की मात्रा
- प्रदीपन तीव्रता
व्युत्पन्न राशियाँ (Derived Quantities)
वे भौतिक राशियाँ जो मूल राशियों पर निर्भर करती है, व्युत्पन्न राशियाँ कहलाती है।
- क्षेत्रफल:- [ लम्बाई * चौड़ाई ]
- आयतन:- [ लम्बाई * चौड़ाई * ऊँचाई ]
- घनत्व:- [ द्रव्यमान / आयतन ]
- वेग:- [ विस्थापन / समय ]
- चाल:- [ दूरी / समय ]
- त्वरण:- [ वेग में परिवर्तन / समय ]
- बल:- [ द्रव्यमान * त्वरण ]
- कार्य:- [ बल * विस्थापन ]
- संवेग:- [ द्रव्यमान * वेग ]
- शक्ति:- [ कार्य / समय ]
- दाब:- [ बल / क्षेत्रफल ]
- आवेग:- [ बल * समय ]
(iii) पूरक राशियाँ (Dupplimentary Quantities)
ये मूल राशियों के समान ही होती है किन्तु इन्हें बाद में खोजा गया इसलिए ये पूरक राशियाँ कहलाती हैं।
ये दो प्रकार की होती है –
- कोण
- ठोस कोण
भौतिक राशियों का मापन :-
पहले समय में मनुष्य अपनी ज्ञानेन्द्रियो की सहायता से कौन सी वस्तु कितनी लम्बी या छोटी है। आँख से देखकर यह पता लगाते थे या हाथ से छूकर किसी वस्तु के बारे में यह बताया जाता था कि कौन सी वस्तु ठंडी है या गर्म है। किसी वस्तु को हाथ में लेकर यह पता लगाया जाता था कि वस्तु भारी है या हल्की। किन्तु इन सब स्थितियों में वस्तु का सही-सही मापन नहीं किया जा सकता था इसलिए किसी भी वस्तु के सही मापन के लिए दो चीजों की आवश्यकता होती है:-
- इकाई या मात्रक (Unit)
- उपकरण (Instrument)
(1) इकाई
भौतिक राशियों के मापन हेतु निश्चित किए गए संख्यात्मक मान को इकाई कहते हैं।
अब तक वस्तुओं को मापने की निम्न पद्धतियाँ प्रचलित हैं जो कि निम्नलिखित हैं-
- F.P.S. पद्धति [ फुट – पाउण्ड -सैकण्ड ]
- C.G.S पद्धति [ सेन्टीमीटर- ग्राम-सैकण्ड ]
- M.K.S पद्धति [मीटर – किलोग्राम-सैकण्ड ]
- S.I पद्धति
(i) F.P.S. पद्धति
इसे ब्रिटिश पद्धति भी कहा जाता है। यह सबसे पुरानी पद्धति है जो लगभग समाप्त हो चुकी है। इस पद्धति में लम्बाई को फुट (फीट) में, द्रव्यमान को पौंड में व समय को सैकण्ड में मापा जाता है।
(ii) C.G.S.पद्धति
यह पद्धति फ्रांस ने दी थी। इस पद्धति को दशमलव पद्धति या मेट्रिक पद्धति भी कहा जाता है। इस पद्धति में लम्बाई को सेन्टीमीटर में, द्रव्यमान को ग्राम में व समय को सैकण्ड में मापा जाता है।
(iii) M.K.S. पद्धति
यह भी दशमलव पद्धति कहलाती है। इस पद्धति में लम्बाई को मीटर में, द्रव्यमान को किलोग्राम में व समय को सैकण्ड में मापा जाता है।
(iv) S.I. पद्धति
M.K.S. पद्धति में कुछ संशोधन करने के पश्चात एक नई पद्धति काम में लाई गई, जिसे अंतर्राष्ट्रीय पद्धति कहा गया। इस पद्धति में लम्बाई को मीटर में, द्रव्यमान को किलोग्राम में, समय को सेकेण्ड में, ताप को केल्विन, पदार्थ की मात्रा मोल में मापी जाती है।
भौतिक इकाइयाँ दो प्रकार की होती हैं-
- मूल इकाई
- व्युत्पन्न इकाई
(i). मूल इकाई:- मूल राशियों के मापन के लिए जिन इकाईयों को काम में लिया जाता हैं, मूल इकाइयाँ कहलाती हैं।
ये इकाईयाँ आपस में स्वतन्त्र होती हैं।
| मूल राशियाँ | मूल इकाई | संकेत (Symbol) |
|---|---|---|
| लम्बाई | मीटर | m |
| द्रव्यमान | किलोग्राम | kg |
| समय | सैकण्ड | S या Sec. |
| ताप | केल्विन | K |
| विद्युत धारा | ऐम्पियर | A |
| पदार्थ की मात्रा | मोल | mol |
| प्रदीपन तीव्रता | कैण्डेला | cd |
(ii) व्युत्पन्न इकाई:- व्युत्पन्न राशियों के मापन के लिए जिन इकाइयों को काम में लेते हैं, उन्हें व्युत्पन्न इकाईयाँ कहते हैं।
व्युत्पन्न इकाईयाँ मूल इकाईयों पर आधारित होती है।
जैसे-
वेग = मीटर/ सैकण्ड
त्वरण = मीटर / सेंकण्ड2
चाल = मीटर / सैकण्ड
विमाएँ तथा विमिय समीकरण
विमा
किसी व्युत्पन्न राशि को मूल राशि में व्यक्त करने पर मूल राशियों पर लगी घातें, उस व्युत्पन्न राशी की विमाएँ कहलाती है।
- लम्बाई की विमा = L
- द्रव्यमान की विमा = M
- समय की विमा = T
- विद्युत धारा की विमा = A
- ताप की विमा = K
- कोण की विमा = θ
जबकि किसी व्युत्पन्न राशी को MaLbTc के रूप में लिखा जाये तो यह एक विमीय समीकरण कहलाता है।
जैसे– बल का विमिय समीकरण [F] = [ M’L’ T-2]
सार्वत्रिक गुरुत्वीय नियतांक [G] का विमिय समीकरण –
\(F = \frac{Gm_1m_2}{r^2}\)
[ M-1L3T-2] = [ G ]
विभिन्न भौतिक राशियाँ, उनके मूल राशियों से सम्बन्ध तथा विमीय सूत्र :-
| क्र.सं. | भौतिक राशि | अन्य राशियों से सम्बन्ध | विमीय सूत्र | S.I. पद्धति में मात्रक |
|---|---|---|---|---|
| 1 | लम्बाई, चौड़ाई, ऊँचाई विस्थापन (l) | – | [M0L1T0] | m |
| 2 | क्षेत्रफल (A) | लम्बाईx लम्बाई | [M0L2T0] | m2 |
| 3 | आयतन (V) | लम्बाई x ल x ल | [M0L3T0] | m3 |
| 4 | वेग (v) | विस्थापन/समय | [M0L1T-1] | m/s |
| 5 | त्वरण (a), गुरुत्वीय त्वरण (g) | वेग में परिवर्तन / समय | [M0L1T-2] | m/s2 |
| 6 | घनत्व (d) | द्रव्यमान/आयतन | [M1L-3T0] | Kg/m3 |
| 7 | रैखिक संवेग (P) | द्रव्यमान x वेग | [M1L1T-1] | Kg m/s |
| 8 | बल (F) | द्रव्यमान x त्वरण | [M1L1T-2] | Kg m/s2=N |
| 9 | आवेग( J या I ) | बल x समय | [M1L1T-1] | Ns |
| 10 | दाब (P) | बल / क्षेत्रफल | [M1L-1T-2] | N/m2 |
| 11 | सार्वत्रिक गुरुत्वीय नियतांक (G) | G=(Fxr2)/(m1m2) | [M-1L3T-2] | N m2/kg2 |
| 12 | कार्य (W), ऊर्जा(E) | बल X विस्थापन | [M1L2T-2] | J |
| 13 | शक्ति (P) | कार्य / समय | [M1L2T-3] | W |
| 14 | पृष्ठ तनाव(T) | बल / लम्बाई | [M1L0T-2] | N/m |
| 15 | बल नियतांक(K) | बल / विस्थापन | [M1L0T-2] | N/m |
| 16 | घूर्णन त्रिज्या या परिभ्रमण त्रिज्या (k) | दूरी | [M0L1T0] | m |
| 17 | जड़त्व आघूर्ण(I) | द्रव्यमान X दूरी2 | [M1L2T0] | Kg m2 |
| 18 | आवृति(r) | कम्पन/समय | [M0L0T-1] | Hz |
| 19 | कोण ( θ ) | चाप / त्रिज्या | [M0L0T0] | rad |
| 20 | कोणीय वेग(w) | कोण/समयान्तराल | [M0L0T-1] | rad/s |
| 21 | कोणीय त्वरण (a) | कोणीयवेग / समयान्तराल | [M0L0T-2] | rad/s2 |
| 22 | कोणीय संवेग (J,L) | संवेगxलंबबत दूरी | [M1L2T-1] | Kg m2/s |
| 23 | बलयुग्म अथवा बल आघूर्ण | बलxलंबबत दूरी | [M1L2T-2] | Nm |
| 24 | प्रतिबल | प्रतिक्रियात्मक बल/क्षेत्रफल | [M1L-1T-2] | N/m2 |
| 25 | विकृति | विन्यास में परिवर्तन / प्रारंभिक विन्यास | [M0L0T0] | कोई नहीं |
| 26 | प्लांक स्थिरांक(h) | ऊर्जा/आवृति | [M1L2T-1] | Js |
| 27 | वेग प्रवणता | वेग/दूरी | [M0L0T-1] | S-1 |
| 28 | प्रत्यास्था गुणांक | प्रतिबल/विकृति | [M1L-1T-2] | N/m2 |
| 29 | तरंगदैर्ध्य | दूरी | [M0L1T0] | m |
| 30 | दाब प्रवणता | दाब/दूरी | [M1L-2T-2] | N/m3 |
| 31 | श्यानता गुणांक(n) | बल/(क्षेत्रफलxवेग प्रवणता) | [M1L-1T-1] | Ns/m2 |
| 32 | पृष्ठ ऊर्जा घनत्व | ऊर्जा/क्षेत्रफल | [M1L0T-2] | J/m2 |
| 33 | दाब ऊर्जा | दाबxआयतन | [M1L2T-2] | J |
| 34 | विशिष्ट ऊष्मा | ऊर्जा/(द्रव्यमानx ताप वृद्धि) | [M0L2T-2K-1] | J/kgK |
| 35 | ऊष्माधारिता, एन्ट्रॉपी | द्रव्यमानxविशिष्ट ऊष्मा | [M1L2T-2K-1] | J/K |
| 36 | स्टीफन नियतांक | ऊर्जा/(क्षेत्रफलxसमयxताप) | [M1L0T-3K-4] | Jm-2s-1k-4 |
| 37 | बोल्ट्ज़मेन नियतांक(K) | गतिज ऊर्जा/ताप | [M1L2T-2K-1] | J/K |
| 38 | गुप्त ऊष्मा | उष्मीय ऊर्जा/द्रव्यमान | [M0L2T-2] | J/kg |
| 39 | सक्रियता(A) | विघटन/समय | [M0L0T-1] | विघटन/S-1 |
| 40 | वीन नियतांक(b) | तरंगदैर्ध्यxतापान्तर | [M0L1T0K1] | mk |
| 41 | आवेश (Q) | धारा x समय | [M0L0T1A1] | C |
| 42 | विभवान्तर (v) | कार्य/आवेश | [M1L2T-3A-1] | V |
| 43 | प्रतिरोध (R) | विभवान्तर/धारा | [M1L2T-3A-2] | Ω |
| 44 | धारिता (c) | आवेश/विभवान्तर | [M-1L-2T4A2] | F |
| 45 | धारा घनत्व(J) | विद्युत धारा/क्षेत्रफल | [M0L-2T0A1] | A/m2 |
| 46 | चालकता (G) | 1/प्रतिरोध | [M-1L-2T3A2] | Ω-1 |
| 47 | विद्युत क्षेत्र | विद्युतबल / आवेश | [M1L1T-3A-1] | N/C |
| 48 | विद्युत फ़्लक्स | विद्युतक्षेत्रxक्षेत्रफल | [M1L3T-3A-1] | Vm |
| 49 | चुंबकीय क्षेत्र(B) | बल/(धारा X लम्बाई) | [M1L0T-2A-1] | T |
| 50 | चुम्बकीय फ्लक्स | चुंबकीय क्षेत्र x क्षेत्रफल | [M1L2T-2A-1] | Wb |
| 51 | चुम्बकीय द्विध्रुव आघूर्ण | बल आघूर्ण/चुंबकीय क्षेत्र | [M0L2T0A1] | Am2 |
Note:- सभी संख्यात्मक मान जैसे – 1,2,3,4,5,_______,n त्रिकोणमित्तिय फलन जैसे- Sin θ, Cos θ, tan θ _ _ _, लघुगणक फलन, चर घातांकी फलन [ex] इन सब की विमा शून्य होती हैं। अर्थात् ये विमाहीन होते हैं।
शुद्ध अनुपात
शुद्ध अनुपात अर्थात् जिसमें अंश व हर दोनों की इकाई समान हो , ये विमाहीन होते हैं, शुद्ध अनुपात कहलाता हैं।
समांगता का सिद्धांत (Principle of Homagenety) :-
इस सिद्धांत के अनुसार “किसी भौतिक राशि के दोनों पक्षों के प्रत्येक पद की विमा समान होनी चाहिए।”
विमा के अनुप्रयोग (Application of Dimension)
- विभिन्न भौतिक राशियों के मध्य सम्बन्ध स्थापित करना
- विभिन्न अज्ञात भौतिक राशीयों की विमा ज्ञात करना
- किसी भौतिक राशि को एक इकाई से दूसरी इकाई मे परिवर्तित करना
विमा तथा विमिय समीकरण की सीमाएँ :-
- कुछ भौतिक राशियों के नाम अलग-अलग होने पर भी उनका विमिय समीकरण एक समान होता है अर्थात् हम विमा के आधार पर इन भौतिक राशियों को अलग-अलग नहीं कर सकते।
- जैसे:- कार्य, ऊष्मा व ऊर्जा इन तीनों की विमा समान होती है जबकि ये तीनों ही अलग-अलग है।
- विमाहीन नियतांक की हम विमा ज्ञात नहीं कर सकते।
- शुद्ध अनुपात वाली भौतिक राशियों की विमा ज्ञात नहीं की जा सकती।
- जैसे:- कोण, विकृति ।
सार्थक अंक (Significant figure)
किसी भौतिक राशी को शुद्धता के साथ लिखने के लिए जितने अंकों की आवश्यकता होती है, वे अंक सार्थक अंक कहलाते हैं।
सार्थक अंक ज्ञात करने के लिए हम निम्नलिखित नियम काम में लेते हैं –
- सभी अशून्य के अलावा शून्य अंक सार्थक अंक नहीं कहलाते है।
- यदि किन्हीं दो अशून्य अंक के मध्य शून्य आ जावे तो वे शून्य सार्थक अंक कहलाते है।
- दशमलव वाली राशि या एक से छोटी दशमलव वाली किसी राशि में दशमलव के दाँयी ओर व प्रथम अशून्य अंक के बाँयी ओर वाले शून्य सार्थक अंक नहीं कहलाते ।
- एक से छोटी दशमलव वाली संख्या के अन्तिम अशून्य अंक के बाद यदि कोई शून्य आता है तो वह शून्य सार्थक अंक कहलाएगा।
- किसी भौतिक राशि के मापन में दशमलव की स्थिति बदलने पर सार्थक अंकों की संख्या अपरिवर्तित रहती है।
- किसी भौतिक राशी के मापन में यदि उसका मान दस की घात में आए तो दस की घात को सार्थक अंक नहीं माना जाता।
- यदि किसी भौतिक राशि को एक पद्धति से दूसरी पद्धति में बदला जाता है तो सार्थक अंकों की संख्या अपरिवर्तित रहती है।
संख्या को पूर्णांकित करना (Rounding off a digit)
किसी दशमलव वाली संख्या मे मान को निश्चित करने के लिए कुछ अंक छोड़े जाते है। ऐसा करना संख्या को पूर्णांकित करना कहलाता है।
संख्या को पूर्णांकित करने के कुछ नियम :-
- यदि किसी दशमलव संख्या में पीछे के एक अंक को छोड़ना हो , यदि वह अंक पाँच से बड़ा हो तो आगे वाले अंक में एक जोड़ देते है।
- यदि किसी दशमलव संख्या में पीछे के एक अंक को छोड़ना हो, यदि वह अंक 5 से छोटा हो तो आगे वाला अंक अपरिवर्तित रहता है।
- यदि किसी दशमलव संख्या में पीछे के एक अंक को छोड़ना हो, यदि वह अंक 5 ही हो तो छोड़े जाने वाले अंक के ठीक पहले वाले अंक को देखते है यदि वह सम है तो यह पहले वाला अंक अपरिवर्तित रहता है।
- यदि किसी दशमलव संख्या में पीछे के एक अंक को हटाना हो, यदि वह अंक 5 ही हो तो उससे अगले वाला अंक विषम होने पर उसमें एक जुड़ जाता है तथा पीछे वाला अंक हट जाता है।
- यदि किसी दशमलव संख्या में पीछे के दो अंक को हटाना हो, यदि वो पीछे के अंक 50 से कम हो तो आगे वाली संख्या अपरिवर्तित रहती है व पीछे के दो अंक हट जाते हैं।
- यदि किसी दशमलव संख्या में पीछे के दो अंक को छोड़ना हो, यदि वे अंक 50 से अधिक हो तो आगे वाले अंक में एक जुड़ जाता है तथा पीछे के दो अंक हट जाते हैं।
- यदि किसी दशमलव वाली संख्या में पीछे के दो अंकों को हटाना हो , पीछे के दो अंक 50 ही हो तो आगे वाला अंक सम होने पर यह अपरिवर्तित रहता है तथा पीछे के दो अंक हट जाते है जैसे:-
- यदि किसी दशमलव संख्या में पीछे के दो अंकों को हटाना हो यदि पीछे के दो अंक 50 ही हो तो आगे वाला अंक विषय होने पर उसमें एक जुड़ जाता है तथा पीछे के दो अंक हट जाते है।
गणितीय संक्रियाएँ जोड़ व बाकी की (सार्थक अंकों के साथ)
जोड़
जब दो या दो से अधिक दशमलव वाली संख्या को जोड़ा जाता हो तो हम देखते है कि जोड़े जाने वाली संख्याओं में दशमलव के बाद Minimum (न्यूनतम) सार्थक अंकों की संख्या कितनी है। तो इनके परिणाम में भी दशमलव के बाद न्यूनतम सार्थक अंक होने चाहिए।
माना किसी जुड़ने वाली दशमलव संख्याओं में एक संख्या के दशमलव के बाद न्यूनतम सार्थक अंक n है तो इन सब संख्याओं के परिणाम में भी दशमलव के बाद सार्थक अंकों की संख्या n होगी।
Note:- दशमलव संख्याओं के घटाने में भी इन्हीं नियमों का पालन होगा। जैसा जोड़ में हुआ है।
भाग व गुणा
जिन दो राशियों का गुणा या भाग करना है। माना उनमें न्यूनतम सार्थक अंक n है तो प्राप्त होने वाले परिणाम में भी न्यूनतम कुल सार्थक अंकों की संख्या n होने चाहिए।
मापन में यथार्थता व परिशुद्धता
- कभी-कभी किसी वस्तु का मापन करने में बहुत-सी दिक्कतें आती है जिसके कारण एक ही वस्तु के भिन्न-भिन्न पाठ्यांक प्राप्त होते है।
- प्रत्येक वस्तु का वास्तविक मान होता है। यदि कोई पाठ्यांक वास्तविक मान के सन्निकट हो तो वह पाठ्यांक उसका यर्थाथ मान कहलाता है ।
- जबकि किसी वस्तु का परिशुद्धता से मतलब यह है कि आपने दशमलव के बाद मापन कितनी सीमा तक किया है।
मापन में त्रुटि
प्रत्येक वस्तु का एक वास्तविक मान होता है। जब उसी वस्तु का प्रेक्षित मान वास्तविक मान से भिन्न प्राप्त होता है तो मापन में त्रुटि उत्पन्न होती है। अर्थात् हम यह कह सकते है, कि वास्तविक मान व प्रेक्षित मान का अन्तर, मापन में त्रुटि कहलाता है।
यदि किसी वस्तु का वास्तविक मान (True Value) नहीं दिया गया हो तो हम वास्तविक मान की जगह औसत मान लेकर चलते है। औसत मान निकालने के लिए हम लिए गए, सभी प्रेक्षित मानों को जोड़कर उसमें प्रेक्षित मानों की संख्या का भाग देते हैं।
मापन में त्रुटि उत्पन्न होने के कारण
- जिस उपकरण से मापन किया है वह उपकरण खराब हो। जिससे लिये गये प्रेक्षित मान वास्तविक मान से भिन्न प्राप्त होंगे।
- किसी-किसी वस्तु का मापन आसपास के वातावरण पर निर्भर करता है जिसके कारण भी मापन में त्रुटि उत्पन्न होती है।
- कभी-कभी सावधानीपूर्वक मापन नहीं लेने पर उस मापन में त्रुटि उत्पन्न हो जाती है।
- इन तीनों कारणों को हम अपनी समझ से दूर कर सकते हैं। इसलिए इन त्रुटियों को क्रमबद्ध त्रुटि कहते है।
- ऐसी त्रुटि जो हमें नहीं पता कि यह किन कारणों से उत्पन्न हुई है, उसे यादृच्छ त्रुटि (Random) कहते है।
मुख्यत: त्रुटि चार प्रकार की होती है:-
1. परम त्रुटि / निरपेक्ष त्रुटि (Absolute Error):- वास्तविक मान तथा प्रेक्षित मान का अन्तर, परम त्रुटि कहलाती है।
परम त्रुटि का मान धनात्मक या ऋणात्मक हो सकता है।
2. माध्य परम त्रुटि (Mean absolute Error):- इसे सभी परम त्रुटि के धनात्मक मानों का औसत निकालकर ज्ञात किया जाता है।
3. सापेक्ष त्रुटि (Relative or Fractional Error):- यह माध्य परम त्रुटि व वास्तविक मान का अनुपात होती है।
4. प्रतिशत त्रुटि / % त्रुटि (Percentage Error):-
% त्रुटि = \(\frac{Δa_m}{a_m}×100\)
त्रुटियों का संयोजन
जब हमें किन्हीं दो अलग-अलग राशियों में त्रुटि पता है तो जब इन राशियों को आपस में जोड़ा/घटाया/ गुणा / भाग किया जावे तो प्राप्त होने वाले परिणाम में भी त्रुटि होगी।
इसे निम्न प्रकार से ज्ञात किया जाता है –
1. दो राशियों की जोड़ में :-
± Δx = ± (Δa + Δb)
2. दो राशियों की बाकी में
± Δx = ± (Δa + Δb)
Note:- अतः राशियों की जोड़ या उनकी बाकि में त्रुटि सदैव जुड़ती है।
3. राशियों का गुणा
\(±\frac{∆x}{x} = ±\frac{∆a}{a} ± {∆b}{b}\)
4. राशियों का भाग:-
\(±\frac{∆x}{x} = ±\frac{∆a}{a} ± {∆b}{b}\)
Practicle unit
जब हम किसी भौतिक राशि की इकाई उसकी स्थिति देखकर बनाते है तो इकाईयाँ Practicle units कहलाती है।
लम्बी दूरी की इकाईयाँ :-
1. एक A.U. (Astronomide unit) खगोलीय इकाई:- सूर्य व पृथ्वी के बीच की औसत दूरी 1 A.u. कहलाती है।
1 A.u. = 1.496 x 1011m
2. एक प्रकाश वर्ष (Light year):- कोई प्रकाश एक वर्ष में जितनी दूरी तय करता है वह दूरी एक प्रकाश वर्ष कहलाती है।
1 ly = 9.46 X 1015 m
3. एक पार-सेक (Par-Sec) (Paralletic – Second):- यदि एक A.u. दूरी पर स्थित दो उपग्रह किसी बिन्दू पर 1 सेकण्ड का कोण बनाते है तो उस बिन्दु व उपग्रह के बीच की दूरी, 1 पार-सेक कहलाती है।
1 पार-सेक = 3.084 X1016 m
अति सूक्ष्म दूरियाँ
- माइक्रोमीटर (Micro meter) = 1um = 10-6 m
- नैनोमीटर (nona – meter) = 1nm = 10-9 m
- पीको मीटर (1pm) = 1pm = 10-12 m
- ऐंग्स्ट्रॉन [ Å ] = 1 Å = 10-10 m
- फर्मी (Fermi) or (Fecto) = 1 fermi = 10-15 m
क्षेत्रफल से सम्बन्धित इकाईयाँ :-
- 1 एकड़ = 4047 m²
- 1 हेक्टेयर = 104 m²
लम्बी दूरी का मापन (वृहद दूरी का मापन)
लम्बन विधि
इस विधि की सहायता से हम लम्बी दूरियों का मापन करते है। जैसे- पृथ्वी की सतह से कोई उपग्रह कितनी दूरी पर स्थित है इस विधि से ज्ञात किया जाता है इसलिए इस विधि को लम्बन विधि भी कहते है।
किसी आकाशीय पिंड का व्यास ज्ञात करना :-
(उपग्रह का व्यास ज्ञात करना ) –
लम्बन विधि की सहायता से हम किसी भी आकाशीय पिंड का आकार व उस पिंड की पृथ्वी से दूरी ज्ञात कर सकते हैं।
अतिसूक्ष्म दूरियों का मापन
सामान्यतः स्केल की सहायता से हम छोटी से छोटी 1 mm की लम्बाई माप सकते है। अत: इस स्केल का अल्पत मान 1 mm या 0.1 cm होगा। वर्णियर कैलीपर्स की सहायता से हम छोटी से छोटी 0.01cm लम्बाई माप सकते है व पेंचमापी की सहायता से 0.001 cm तक की सूक्ष्म लम्बाई माप सकते है। परमाणु का आकार 10-8m या 10-10m की कोटि का होता है इसको मापने के लिए हम एक विशेष विधि का उपयोग लेते है। इस विधि की सहायता से परमाणु का आकार या उसके नाभिक का आकार मापा जा सकता है।
वर्णीयर कैलीपर्स

- वैज्ञानिक वर्णीयर ने 1mm से भी छोटी दूरी का मापन करने के लिए एक उपकरण बनाया। इस उपकरण की सहायता से हम मुख्य स्केल के 1mm भाग का दसवां भाग तक का मापन शुद्धता के साथ कर सकते है।
- वर्णीयर कैलीपर्स में मुख्य स्केल के नौ भाग व वर्णीयर कैलीपर्स के दस भाग आपस में बराबर होते है।
- वर्णीयर कैलीपर्स का अल्पतमांक- किसी भी उपकरण का अल्पतमांक वह मान होता है जो उस उपकरण का सबसे छोटे से छोटा भाग होता है।
- जैसे:- मुख्य स्केल में छोटे से छोटा भाग 1 mm होता है तो यह मुख्य स्केल का अल्पतमांक कहलायेगा।
वर्गीयर कैलीपर्स का अल्पतमांक = मुख्य पैमाने के एक भाग का मान / वर्णीयर स्केल के भागों की संख्या = 0.1 cm /10 = 0.01 cm
पेचमापी (स्क्रूगेज)
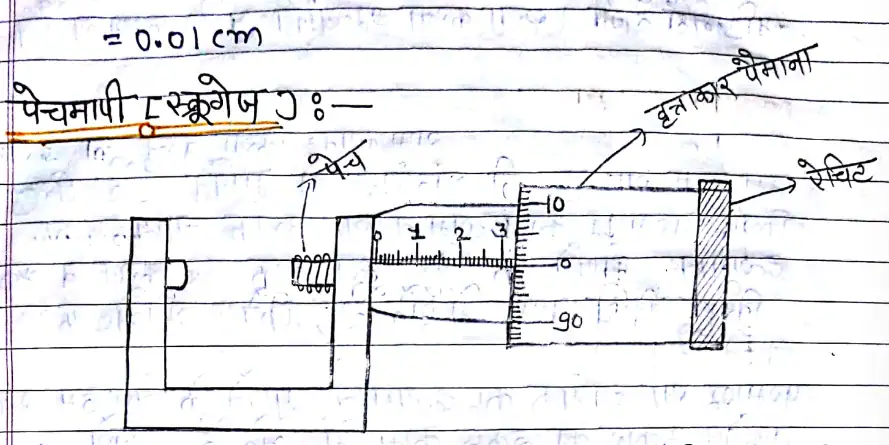
- पेचमापी पेच के सिद्धान्त पर कार्य करता है इसलिए इसे पेचमापी कहते है।
- पेचमापी में दो पैमाने होते है, पहला मुख्य पैमाना, दूसरा वृताकार पैमाना।
- मुख्य पैमाना सामान्य स्केल का जो पैमाना होता है वही है जबकि वृताकार पैमाने पर 100 समान भाग अंकित होते है।
पेचमापी का अल्पतमांक = चुड़ी अन्तराल / वृताकार पैमाने पर भागों की संख्या = 0.1cm/100 = 0.001cm
चुड़ी अन्तराल:- वृताकार पैमाने को एक पूर्ण चक्र तक घूमाने पर, मुख्य स्केल का पाठ्यांक, चुड़ी अन्तराल कहलाता है |
शून्यांकी त्रुटि:- जब मुख्य स्केल का शून्य व वृताकार स्केल का शून्य आपस में सम्पाती हो जाये तो उपकरण में कोई त्रुटि नहीं होगी। ऐसा करना शून्यांकी त्रुटि कहलाता है।
द्रव्यमान का मापन
सामान्यतः किसी वस्तु का द्रव्यमान हम तुला या बाट की सहायता से मापते है । किन्तु किसी परमाणु का द्रव्यमान या उसके नाभिक का द्रव्यमान मापने के लिए हम एक उपकरण व एक विशेष विधि काम में लेते है, जिसे स्पेट्रोग्राफ कहते है।
परमाणु या नाभिक का द्रव्यमान मापने के लिए हम एक विशेष प्रकार की इकाई काम में लेते है, जिसे a.m.u. या परमाणु द्रव्यमान इकाई कहते हैं।
- 1 a.m.u. = 6C12 के समस्थानिक के एक परमाणुक द्रव्यमान
- 1 a.m.u. = 1.6 x 10-27 kg
- द्रव्यमान की सबसे बड़ी इकाई चन्द्रशेखर सीमा होती है।
- 1 चन्द्रशेखर सीमा= 1 C.S.L. = 1.4 x mass of sun = 1.4 x 2 x 1030 kg = 2.8 x 1030 kg
समय का मापन
पुराने समय में स्प्रिंग वाली घड़ियाँ काम में ली जाती थी। इन घड़ियों के समय के मापन में कुछ न कुछ त्रुटि होती थी। बाद में क्वार्टज घड़ियाँ काम में आने लगी। ये घड़ियां स्प्रिंग घड़ियों की तुलना में अधिक शुद्धता के साथ समय का मापन करती थी।
अंतर्राष्ट्रीय जगहों पर जिन घड़ियों से समय का मापन होता है, उन्हें परमाण्विक घड़ियाँ कहते है। भारत में कुल चार परमाण्विक घड़ियाँ काम में लेते है जिसका नाम CS-133 है। इन घड़ियों से समय के मापन में त्रुटि बहुत कम होती है।
इस प्रकृति में चार मौलिक बल पाए जाते है –
- गुरुत्वाकर्षण
- विद्युत चुम्बकीय बल
- प्रबल नाभिकीय बल
- दुर्बल नाभिकीय बल
Tagged with: class 11 physics chapter 1 ncert notes in hindi | Class 11 physics Chapter 1 Notes in Hindi | physics chapter 1 class 11 notes in hindi | physics class 11 chapter 1 in hindi notes | units and measurement Notes in Hindi

Please give me notes
physics ka chapter 3 ka not
Hindi mudium NEET free all subjects notes